[A] Graphen

[nep]

*UNDER CONSTRUCTION*

1 Einleitung

Natürlicherweise werden sich einige bestimmt fragen, was ein Graph denn überhaupt ist. Eine einfache Definition besagt folgendes:
Ein Graph G besteht aus

• einer Menge von Knoten
• und einer Menge von Knotenpaaren, welche auch Kanten genannt werden.

Bestimmt kennt jeder das "Haus vom Nikolaus":

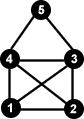
Die Knotenmenge wäre hier {1, 2, 3, 4, 5}, und bildet zusammen mit den Kanten { (1,2), (1,3), (1,4), (2,4), (2,3), (3,4), (3,5), (4,5) } einen Graphen.
Wichtig ist hier zu verstehen, dass das was man im obigen Bild gesehen hat ("Haus vom Nikolaus") lediglich ein Diagramm dieses Graphen darstellt. In einem Diagramm werden die Knoten durch Punkte repräsentiert und die Kanten durch Bögen (=Linien, welche aber nicht unbedingt geradlinig sein müssen). D.h. der eigentliche Graph wird, wie schon erwähnt durch die Knotenmenge und die Kanten repräsentiert.
Andere Beispiele für Graphen sind aber auch Dinge wie Straßenpläne, Fahrpläne, Netwerktopologien, und vieles mehr. Wie man sieht sind Graphen nicht nur etwas theoretisches, sondern haben auch sehr starken Praxisbezug. Insbesondere in der Informatik wird man immer wieder auf Probleme treffen, die man auf graphentheoretische Probleme reduzieren kann. Das ist auch einer der Nutzen von Graphen: Gegebene Objekte und deren Beziehungen werden auf das Wesentliche reduziert, womit man ein höheres Abstraktionsniveau erreicht.
Es ist z.B. möglich jede endliche Menge mit n Elementen auf die Zahlen 0..n-1 abzubilden (natürlich müsste man das jetzt viel mathematischer fassen, aber ich denke das sollte wohl offensichtlich sein). Wenn man z.B. einen Fahrplan hat, könnte man sich folgende Abbildung vorstellen:
Schillerstraße 0
Goethestraße 1
Parkstraße 2
Schlossallee 3
... ...

Es gibt unterschiedliche "Typen" von Graphen. In diesem Artikel werden wir nur sog. einfache Graphen betrachten: Ein Graph heißt einfach wenn er

• eine endliche Knotenmenge besitzt
• keine Knoten mit sich selbst verbunden sind (sog. Schlingen)
• und je 2 Knoten mit höchstens einer Kante verbunden sind.

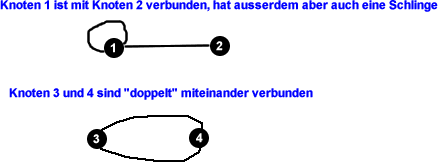
Hier noch ein paar wichtige Definitionen, die immer mal wieder im weiteren Verlauf des Artikels auftauchen werden.

Ordnung eines Graphen G: Unter der Ordnung eines Graphen G versteht man die Anzahl an Knoten in diesem Graphen. Man bezeichnet die Ordnung eines Graphen G auch mit v(G). (v = vertex). Für das "Haus vom Nikolaus" gilt z.B. v(G) = 5.

Größe eines Graphen G: Unter der Größe eines Graphen G versteht man die Anzahl der Kanten in diesem Graphen. Man bezeichnet die Größe eines Graphen G auch mit e(G). (e = edge). Für das "Haus vom Nikolaus" gilt z.B. e(G) = 8.

Ein Graph G mit v Knoten und e Kanten wird auch mit G(v,e) bezeichnet.

Adjazenz: Wenn es zwischen 2 Knoten eine Kante gibt, so heißen die beiden Knoten benachbart (=adjazent).
Unter dem Grad eines Knotens v versteht man die Anzahl der Knoten, die mit v benachbart sind. Man bezeichnet den Grad eines Knotens v auch mit d(v).
Im "Haus von Nikolaus" sind offensichtlich z.B. die Knoten 1 und 2 benachbart. Der Grad von Knoten eins beträgt 3, da dieser mit 3 anderen Knoten benachbart ist, d.h. d(1) = 3.

Weg: Ein Graph mit den Knoten 0..n und den Kanten (0,1), (1,2), …, (n-1,n) wird mit Pn bezeichnet und heißt Weg der Länge n.
Beispiel (P4):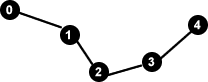

Ist vielleicht etwas viel auf einmal, aber eigentlich sind die Dinge die sich hinter diesen Begriffen verbergen relativ einfach und logisch. Man muss sie sich halt nur merken (oder nachschauen ).

Zusammenfassung:
Ein Graph ist eine Menge von Knoten und Knotenpaaren. Der Graph G(4,4) könnte z.B. so aussehen: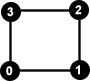

Die Knotenmenge ist dabei { 0, 1, 2, 3 }.
Die Menge von Knotenpaaren (=Kanten) ist dabei { (0,1), (1,2), (2,3), (3,0) }.
Der Grad eines jeden Knotens ist dabei 2. D.h. es gilt d(0) = d(1) = d(2) = d(3) = 2.

Übrigens ist dieser Graph auch ein Weg, und zwar ein Weg der Länge 3.

Hier noch ein paar Beispiele für Graphen:

BILDER

2 Gleichheit von Graphen, Teilgraphen und Zusammenhänge

In diesem Abschnitt wollen wir uns weiter mit Graphen und einigen ihrer Eigenschaften vertraut machen, um einfach ein besseres „Gefühl“ dafür zu bekommen, bevor wir dann im nächsten Abschnitt endlich auch mal etwas programmieren werden.

Betrachten wir folgenden einfachen Graphen G1:

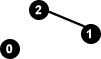
Die Knotenmenge ist hier { 0, 1, 2 } und die Kantenmenge ist { (1,2) }.

Jetzt wollen wir einen „ähnlichen“ Graphen G2 betrachten:

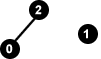
Die Knotenmenge ist auch hier { 0, 1, 2 }. Die Kantenmenge ist jedoch { (0,2) }.

Die Kantenmengen der beiden Graphen unterscheiden sich offensichtlich. Also sind die beiden Graphen auch nicht gleich. Oder doch?
Wenn man von der reinen Definition von Gleichheit ausgeht, dann sind sie tatsächlich nicht gleich. Die beiden Graphen sind sich jedoch sehr ähnlich, genauer gesagt: Sie sind isomorph. In unserem Sprachgebrauch verwenden wir die Begriffe "gleich" und "isomorph" oft synonym, obwohl dies eigentlich nicht stimmt.
Isomorph bedeutet hier: Die Graphen G1 und G2 können so nummeriert werden, dass die Kantenmengen von G1 und G2 übereinstimmen:
(Wir nummerieren einfach G2 um, und schon stimmen auch die Kantenmengen überein):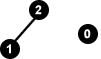

Ein anderes Beispiel hierfür:

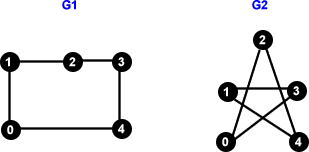
Auch wenn die Graphen auf den ersten Blick nicht isomorph aussehen, so sind sie es doch. Durch eine geeignete Umnummerierung erreicht man für beide Graphen dieselbe Kantenmenge. Dies sei dem Leser als Übung überlassen. Wir wollen auch nicht viel tiefer hinein steigen in dieses Thema, denn alleine darüber könnte man schon einen Artikel füllen. Es ist jedoch wichtig zu verstehen was Isomorphie bedeutet. In Diagramm-Darstellungen von Graphen verzichtet man übrigens oft auf eine explizite Nummerierung, da verschiedene Nummerierungen doch nur wieder zu isomorphen Graphen führen.
Jedenfalls sei hier noch erwähnt, dass es bis heute kein wirklich praktikables Verfahren gibt um möglichst schnell herauszufinden ob 2 Graphen isomorph sind oder nicht. Es gibt zwar einige Verfahren, jedoch ist es oft ein Leichtes einen Graphen zu konstruieren, für welchen ein solches Verfahren nicht anwendbar ist. D.h. wenn man herausfinden will, ob 2 Graphen isomorph sind, bleibt einem im Prinzip nichts anderes übrig als alle möglichen Kombinationen auszuprobieren. Für einen Graphen mit beispielsweise nur 100 Knoten müsste man alle Permutationen der Knotennummern 0 bis 99 durchführen. Die Anzahl der Permutationen würde in diesem Fall dann 100! betragen, was eine *verdammt* große Zahl ist

Die Definition eines Teilgraphen ist sehr simpel und straightforward:
Ein Graph H wird genau dann als Teilgraph eines Graphen G bezeichnet, wenn die Knoten- und Kantenmengen von H Teilmengen der Knoten- und Kantenmenge von G sind.
Beispiel: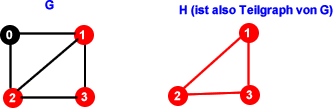

Das führt uns auch sofort zur nächsten Definition:
Einen Graphen nennt man zusammenhängend, wenn es für je 2 Knoten i und j stets einen Weg von i nach v gibt. (Wer nicht mehr weiß was noch mal ein Weg war, kann ja hochblättern).
Auch das ist sehr einfach. Beispiel: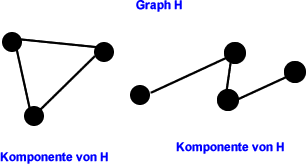

In Bild 2 zerfällt der Graph H in zwei sog. Komponenten. Zusammenhängende Teilgraphen von einem Graphen H, die in keinem anderen Teilgraphen von H enthalten sind, heißen Komponenten. Hört sich evtl. komplizierter an als es ist. Wenn man sich nicht mehr erinnern kann was eine Komponente ist, sollte man sich einfach obiges Bild in Erinnerung rufen. Der gezeigte Graph H war also natürlich nicht zusammenhängend.
In der Praxis ist es oft wichtig zu bestimmen, ob ein Graph nun zusammenhängend ist oder nicht, und in welche Komponenten er zerfällt. Wenn z.B. ein Computernetzwerk aus mehr als einer Komponente besteht, so weiß man, dass zwischen diesen beiden Komponenten kein Fluss (also keine Verbindung) besteht. Man mag sich jetzt vielleicht denken, dass es doch recht einfach ist, zu bestimmen, ob ein Graph nun zusammenhängend ist oder nicht. Wenn man aber tausende von Knoten hat, dann ist das doch nicht so einfach, und auf keinen Fall mehr mit dem bloßen Auge machbar.
Wir werden im übernächsten Abschnitt ein Verfahren kennen lernen, mit welchem man den Zusammenhang eines Graphen bestimmen kann. Doch zuerst müssen wir erst einmal wissen, wie man einen Graphen überhaupt implementieren kann.

3 Graphen als Datenstruktur

Nachdem wir nun schon einiges über Graphen erfahren haben, wollen wir uns nun Gedanken machen wie wir einen Graphen mittels C++ darstellen könnten.
Um gleich eines vorwegzunehmen: Hierfür gibt es verschiedene Möglichkeiten und auch für jede Möglichkeit wieder unterschiedliche Implementierungen. Wir wollen an dieser Stelle 2 mögliche Implementierungen betrachten, von welchen wir dann eine in C++ umsetzen werden.

Aber zuerst einmal sollte man sich Gedanken machen, welche Basis-Funktionalität unsere Implementierung überhaupt benötigt:

• Man muss auf jeden Fall die Knotenmenge festlegen können
• Man muss eine Kante zwischen 2 Knoten einfügen können
• Man muss eine Kante zwischen 2 Knoten auch wieder entfernen können
• Ausserdem ist es bestimmt sinnvoll testen zu können, ob 2 Knoten benachbart sind

Damit können wir uns schon eine abstrakte Klasse definieren(=Interface), völlig unabhängig von der Implementierung welche wir dann später einsetzen werden bzw. wollen:

//Graph.h
#ifndef _GRAPH_
#define _GRAPH_

#include <set>
using std::set;

class Graph
{

public:

	virtual bool add(unsigned v1, unsigned v2) = 0; //Fügt Kante zwischen Knoten v1 und v2 hinzu
	virtual bool remove(unsigned v1, unsigned v2) = 0; //Entfernt Kante zwischen Knoten v1 und v2
	virtual bool hasEdge(unsigned v1, unsigned v2) const = 0; //Prüft ob eine Kante zwischen v1 und v2 existiert
	virtual const set<unsigned>& getAdjacentNodes(unsigned v) const = 0; //Gibt eine Liste mit allen benachbarten Knoten von v zurück

	virtual unsigned getNumVertices() const = 0; //Gibt die Anzahl von Knoten im Graph zurück
	virtual unsigned getNumEdges() const = 0; //Gibt die Anzahl von Kanten im Graph zurück
};

#endif

Wie man sieht ist die von oben benötigte Funktionalität enthalten und zusätzlich wurden noch 2 weitere Hilfsmethoden hinzugefügt (getNumVertices und getNumEdges).

Wie implementiert man diese Schnittstelle nun? Eine einfache Möglichkeit der Implementierung besteht in der sogenannten

a) Inzidenzmatrix:
Dabei handelt es sich im Prinzip um nichts weiter als um ein 2 dimensionales Array aus Booleans: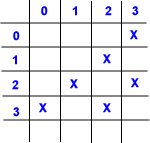

Wenn 2 Knoten i und j miteinander benachbart sind, dann ist das Element in der i-ten Zeile und der j-ten Spalte dieser Matrix „markiert“ (d.h. auf true gesetzt). Im obigen Beispiel hätte man einen Graphen welcher aus 4 Knoten besteht und 3 Kanten besitzt, nämlich folgende: (1,2), (0,3) und (2,3). Alle Knoten welche keine Nachbarn haben, sind in der Matrix an den entsprechenden Stellen auf false gesetzt.
Wenn man einen Graphen mit 10 Knoten hätte, dann bräuchte man selbstverständlich eine 10 x 10 Matrix.
Wenn der Knoten 2 mit dem Knoten 3 benachbart ist, dann ist selbstverständlich auch der Knoten 3 mit dem Knoten 2 benachbart. Deshalb ist sowohl das Element [2][3] als auch das Element [3][2] der Matrix auf true gesetzt.
Ich denke es ist nicht sonderlich schwer das Prinzip der Inzidenzmatrix zu verstehen; auch sollte es nicht schwer sein diese mittels des obigen Interfaces zu implementieren.
Jede Implementierung hat allerdings ihre Vor- und Nachteile, so auch die Inzidenzmatrix: Prinzipiell ist es so, dass die Geschwindigkeit beim Hinzufügen und Entfernen von Kanten schnell ist, da es sich hierbei immer um eine konstante Geschwindigkeit ( O(1) ) handelt (vgl. Zugriffe auf Arrays). Dem gegenüber steht allerdings ein deutlich erhöhter Speicherverbrauch, was sich insbesondere bei dünn besetzten Graphen bemerkbar macht. Hat man einen Graphen von z.B. 1000 Knoten, hat für diesen aber z.B. nur 10 Kanten, dann wird hier *sehr* viel Speicherplatz verschwendet. Anders sieht es bei dicht besetzten Graphen aus: Hier bietet sich eine Implementierung mittels der Inzidenzmatrix durchaus an.

Eine weitere Möglichkeit besteht in der sogenannten

b) Adjazenzliste
Hierbei handelt es sich um ein Array, dessen Elemente Listen sind. Dabei repräsentiert das i-te Array Element einen Knoten. Die Liste in diesem Array Element enthält dann alle Nachbarknoten dieses Knotens. Das ganze sieht dann so aus:

D.h. wenn die Knoten i und j benachbart sind, dann ist die Zahl j in der i-ten Liste (also in der Liste vom i-ten Array Element) enthalten. Auch hier hat man einen Graphen welcher aus 4 Knoten besteht und die gleiche Kantenmenge wie unter a) besitzt.
Eine Adjazenzliste bietet sich für eher dünn besetzte Graphen an, da die Geschwindigkeit hier nicht ganz so gut ist wie bei der Inzidenzmatrix. Allerdings wird der Speicher besser ausgenutzt, was sich eben insbesondere bei dünn besetzten Graphen bemerkbar macht.
Ich habe oben gesagt, dass es sich bei einer Adjazenzliste um ein Array, dessen Elemente Listen sind, handelt. Das stimmt auch von der Kernaussage, allerdings ist es besser anstelle von Listen Mengen zu verwenden. Eine Menge garantiert im Gegensatz zu einer Liste Dublettenfreiheit (d.h. kein Element kommt mehr als einmal vor, und da ein Knoten nicht mehr als einmal mit einem anderen Knoten benachbart sein kann, ist das hier auch genau das richtige). Ausserdem werden einzelne Elemente einer Menge in logarithmischer Zeit gefunden, was eine Effizienzsteigerung im Gegensatz zu Listen darstellt. Da die STL uns eine brauchbare Implementierung einer Menge in Form von std::set bietet, steht einer Implementierung nichts mehr im Wege.
Abschließend sei noch angemerkt, dass wir uns das Leben etwas vereinfachen, indem wir dem Konstruktor initial die Anzahl der Knoten des Graphen initial übergeben müssen. Es sollte für den Leser kein Problem sein, dieses später etwas flexibler zu gestalten, falls gewünscht.

Jetzt aber zur Implementierung:

//GraphImpl.h

#ifndef _GRAPH_IMPL_
#define _GRAPH_IMPL_

#include <set>
#include <vector>
#include <iterator>
#include "Graph.h"
using std::set;
using std::vector;

class GraphImpl : public Graph
{

public:

	bool add(unsigned v1, unsigned v2); //Fügt Kante zwischen Knoten v1 und v2 hinzu
	bool remove(unsigned v1, unsigned v2); //Entfernt Kante zwischen Knoten v1 und v2
	bool hasEdge(unsigned v1, unsigned v2) const; //Prüft ob eine Kante zwischen v1 und v2 existiert
	const set<unsigned>& getAdjacentNodes(unsigned v) const; //Gibt eine Liste mit allen benachbarten Knoten von v zurück

	unsigned getNumVertices() const; //Gibt die Anzahl von Knoten im Graph zurück
	unsigned getNumEdges() const; //Gibt die Anzahl von Kanten im Graph zurück

	GraphImpl(unsigned numVertices);

private:

	vector< set<unsigned> > adjList;
	unsigned numVertices;
	unsigned numEdges;

};

#endif

//GraphImpl.cpp
#include "GraphImpl.h"

GraphImpl::GraphImpl(unsigned numVertices)
{
	numEdges = 0;
	numVertices = numVertices;

	for (unsigned int i=0; i<numVertices; i++)
	{
		adjList.push_back(set<unsigned>());
	}
}

unsigned GraphImpl::getNumVertices() const
{
	return numVertices;
}

unsigned GraphImpl::getNumEdges() const
{
	return numEdges;
}

bool GraphImpl::hasEdge(unsigned v1, unsigned v2) const
{
	set<unsigned>::const_iterator it = adjList.at(v1).find(v2);
	if (it != adjList.at(v1).end())
		return true;
	return false;
}

bool GraphImpl::add(unsigned v1, unsigned v2) 
{
	//Wir unterstützen nur einfache Graphen, d.h. keine Schlingen und keine Mehrfachkanten (-> Einleitung/Definitionen)
	if ( v1 == v2 || hasEdge(v1,v2) ) 
		return false;

	adjList.at(v1).insert(v2);
	adjList.at(v2).insert(v1);

	numEdges++; //Es gibt jetzt eine Kante mehr im Graph

	return true;
}

bool GraphImpl::remove(unsigned v1, unsigned v2)
{
	//Wir können nur tatsächlich existierende Kanten entfernen
	if (hasEdge(v1,v2) == false)
		return false;

	adjList.at(v1).erase(v2);
	adjList.at(v2).erase(v1);

	numEdges--;

	return true;
}

const set<unsigned>& GraphImpl::getAdjacentNodes(unsigned v) const
{
	const set<unsigned>& adjNodes = adjList.at(v);
	return adjNodes;
}

4 Union-Find – Oder wie bestimme ich den Zusammenhang eines Graphen

Bisher haben wir ja nicht viel brauchbares mittels Graphen zustande gebracht. Außer ein paar Definitionen und netten Eigenschaften ist nichts gewesen. Da viele Dinge aus dem tatsächlichen Leben (oder besser gesagt im Bereich der Informatik) sich auf Graphen übertragen lassen, ist es doch oftmals ganz nützlich zu wissen ob ein Graph zusammenhängend ist oder nicht (vgl. Abschnitt !!2!!), womit wir auch beim ersten wirklich brauchbarem „Ergebnis“ wären, nämlich einem Algorithmus um genau dieses zu bestimmen.

[GPC]

Gefällt mir schon sehr gut, v.a. die Erklärungen sind toll (und werden zusätzlich durch die Bilder optisch verdeutlicht). Freue mich schon auf die finale Version.

[Jester]

Sieht echt gut aus. Ich hab ein paar Anmerkungen dazu, die mir beim Lesen aufgefallen sind:

- imho sollte die formale Standarddefinition eines Graphen als Tupel (V,E) mit E Teilmenge VxV nicht fehlen

- Inzidenz (von Knoten und Kanten) ist noch ein wichtiger Grundbegriff

- Deine Inzidenzmatrix ist eine Adjazenzmatrix

Zwei Schreibweisen gefallen mir nicht so gut. Zum einen die einen Graphen mit v Knoten und e Kanten als G(v,e) zu bezeichnen. G(17,24) kann dann ein völlig anderer Graph sein, als zum Beispiel G(17,24). Keine schöne Namensgebung.

Vielleicht könntest Du auch noch gerichtete Graphen erwähnen. Insbesondere wenn Du ungerichtete betrachtest würde ich die Kante zwischen u und v eher mit {u,v} als mit (u,v) bezeichnen. Damit vermeidest Du die Beachtung der Reihenfolge.

Ansonsten:
Ich find's gut, dass hier etwas Theorie passiert! Weiter so.

edit: btw, mal boost::graph angeschaut? Da sind ne ganze Reihe von Algorithmen schon implementiert.

[Gast]

Jester schrieb:

Vielleicht könntest Du auch noch gerichtete Graphen erwähnen. Insbesondere wenn Du ungerichtete betrachtest würde ich die Kante zwischen u und v eher mit {u,v} als mit (u,v) bezeichnen. Damit vermeidest Du die Beachtung der Reihenfolge.

Das ist mir auch aufgefallen. Ich würd auch die geschweiften Klammern verwenden.

[nep]

Jester schrieb:

Sieht echt gut aus. Ich hab ein paar Anmerkungen dazu, die mir beim Lesen aufgefallen sind:

- imho sollte die formale Standarddefinition eines Graphen als Tupel (V,E) mit E Teilmenge VxV nicht fehlen

- Inzidenz (von Knoten und Kanten) ist noch ein wichtiger Grundbegriff

- Deine Inzidenzmatrix ist eine Adjazenzmatrix

Zwei Schreibweisen gefallen mir nicht so gut. Zum einen die einen Graphen mit v Knoten und e Kanten als G(v,e) zu bezeichnen. G(17,24) kann dann ein völlig anderer Graph sein, als zum Beispiel G(17,24). Keine schöne Namensgebung.

Vielleicht könntest Du auch noch gerichtete Graphen erwähnen. Insbesondere wenn Du ungerichtete betrachtest würde ich die Kante zwischen u und v eher mit {u,v} als mit (u,v) bezeichnen. Damit vermeidest Du die Beachtung der Reihenfolge.

Ansonsten:
Ich find's gut, dass hier etwas Theorie passiert! Weiter so.

edit: btw, mal boost::graph angeschaut? Da sind ne ganze Reihe von Algorithmen schon implementiert.

Erst mal danke allgemein für das (positive) Feedback bisher.

Also ich wollte den Artikel auf jeden Fall so schreiben, dass er nicht zu mathelastig wird (bin ja zudem selbst nicht unbedingt der Mathe-Freak ), aber trotzdem doch auch einiges an Theorie vermittelt wird. Nur eben ohne perfekt getrimmte mathematische Definitionen, welche vielleicht nur jeder dritte versteht.

Das fängt halt IMHO schon mit der Definition an. Ich persönlich denke z.B. nicht dass das unbedingt so verständlich für jemanden ist, der noch nie was mit Relationen usw. zu tun hatte, wenn man auf einmal mit der Kreuzmenge und Tupeln kommt. Aber ich denke, jetzt wo du es angsprochen hast, kann es sicherlich auch nicht schaden, dass noch als zusätzliche Definiton anzugeben (und halt als mathematisch genauere Definition zu kennzeichnen).

Zur Schreibweise (u,v) <-> {u,v}.. das hatte ich gar nicht beachtet. Aber das werde ich auf jeden Fall noch nachträglich ändern. Und dazu auch gleich zum Thema gerichtete Graphen: Ja dazu kommt auf jeden Fall auch noch was Was ich nämlich auf jeden Fall noch reinbringen wollte sind Wegfindungen/Optimierungen, sprich hier dann Prim/Kruskal und Dijkstra. Da werd ich das dann auch kurz einführen.

Mit dem G(v,e) hast du natürlich recht (hast ja sowieso mehr Ahnung von Mathe ). Ich persönlich finde die Schreibweise aber trotzdem ganz praktisch und einfach zu verstehen. Sollte dann auf jeden Fall wohl noch genauer erwähnt werden, dass damit kein eindeutiger Graph "beschrieben" wird. Kommt nicht so richtig durch, wie ich beim nochmaligen Lesen bemerkt habe.

[Ben04]

Wenn du besser Grafiken brauchst/willst kann ich dir helfen.

Gib mir einfach eine Skizze von dem was du brauchst und ich mache sie dir.

[rüdiger]

Für die Skizzen kannst du doch das dot-Format benutzen. Könntest du dann auch in dem Artikel kurz beschreiben (oder eben via boost::graph exportieren)

[Jester]

Mit Verlaub, aber die Layouts die dot produziert sind händisch gemachten doch weit unterlegen. Für so kleine Beispielgraphen würd ich's immer selber machen.

[rüdiger]

Die Code-Zeilen sind übrigend für die Darstellung beis 1024x768 zu lang und verzerren so das Layout. Mach bitte kürzere Code-Zeilen, damit der Artikel sich auch auf kleineren Bildschirmen bequem lesen lässt.