AVL-Baum

[Ben04]

Inhaltsverzeichnis

• 1 Vorwort
• 2 AVL-Baum
• 2.1 Rotationen in einem AVL-Baum
• 2.2 Wann rotieren?
• 2.3 Ausbalancieren
• 2.3.1 Knoten mit Balance -2
• 2.3.2 Knoten mit Balance +2
• 2.4 Gewicht anhängen
• 2.5 Einfügen
• 2.6 Löschen
• 2.7 Andere Operationen
• 3 Implementierung
• 3.1 Darstellung
• 3.2 Dump
• 3.3 Debug-Checks
• 3.4 Kopiekonstruktor
• 3.5 Rotationen
• 3.6 Ausbalancieren
• 3.7 Gewicht
• 3.8 Einfügen
• 3.9 Löschen
• 3.10 Andere Operationen
• 3.11 Experimentierkonsole
• 4 Quellen
• 5 Beweise
• 5.1 Allgemeine Formeln
• 5.2 Notation
• 5.3 Rotationsformeln
• 5.4 Ausbalancieren
• 5.4.1 Das Kind hat eine Balance von +1
• 5.4.2 Das Kind hat eine Balance von 0
• 5.4.3 Das Kind hat eine Balance von -1

1 Vorwort

In folgendem Artikel werde ich nur auf die Besonderheiten eines AVL-Baums gegenüber eines einfachen Suchbaums eingehen. Ich gehe davon aus, dass der Leser mit dem einfachen Suchbaum wie er in dem Artikel "Binärer Suchbaum" beschrieben wird, vertraut ist.

2 AVL-Baum

AVL-Bäume sind spezielle binäre Suchbäume. Sie sind nach ihren Erfindern Adelson-Velsky und Landis benannt. Eines der großen Probleme von Suchbäumen ist, sie im Gleichgewicht zu halten und zu verhindern, dass sie zu einer Luxusversion von verketteten Listen ausarten. Dies wäre der Fall, wenn sie sehr stark zu einer Seite hinhängen würden. Diesem Problem haben sich diese Herren gestellt und haben eine Strategie entwickelt, die es dem Baum erlaubt, sich selbst auszubalancieren und den Benutzer dadurch von dieser Sorge befreit.

Wer sich schon mal selbst an einer Strategie versucht hat, wird festgestellt haben, dass man gar nicht einmal sagen kann, ob der Baum entartet ist, solange man nur einen Knoten betrachtet. Betrachtet man aber den gesamten Baum, so muss man sämtliche Knoten betrachten und man verliert den Geschwindigkeitsvorteil gegenüber den meisten alternativen Datenstrukturen. Man wird sich also nicht darum drücken können, in jedem Knoten Informationen abzulegen, welche Aufschluss über das Gleichgewicht des Baumes geben.

Der AVL-Baum speichert in jedem Knoten neben den üblichen Informationen eines jeden Suchbaums auch noch die Differenz der Höhen der beiden Unterbäume. Ob man die Höhe des rechten von der des linken Unterbaums abzieht oder andersherum, spielt keine Rolle. Man muss sich nur auf eine Vorgehensweise einigen und diese konsequent durchziehen. In diesem Artikel werde ich die des rechten von der des linken abziehen. Diese Differenz bezeichnet man auch als Balance.

Falls ein Knoten nur einen oder gar keinen Unterbaum besitzt, so nimmt man für den oder die fehlenden Unterbäume eine Höhe von 0 an.

Da diese Definition nicht für jeden Leser auf Anhieb verständlich sein dürfte, möchte ich sie mit der Hilfe von zwei Beispielen verdeutlichen.

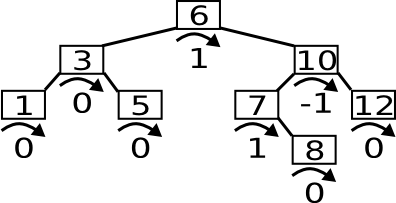
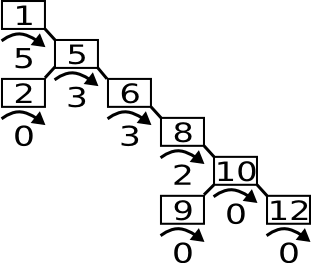
Im ersten Beispiel besitzt die Wurzel zwei Unterbäume. Der linke hat eine Höhe von 2, da er sich über zwei Ebenen erstreckt. Der rechte hat eine Höhe von 3, da es drei Ebenen gibt. Durch das Abziehen der beiden Höhen erhält man die Balance des Knoten nämlich 1.

Der erste Baum ist recht gut ausbalanciert und wesentlich verbessern wird man ihn nicht können. Dies wird dadurch gekennzeichnet, dass die Balancen alle sehr nahe bei 0 liegen. Der perfekte Baum hätte nur Balancen von 0. Wir werden uns aber auch mit -1 und 1 zufrieden geben, da der perfekte Zustand nicht immer realisierbar ist. Ein Baum, der nur Balancen von -1, 0 oder 1 hat, gilt als ausbalanciert.

Der andere Baum dagegen ist stark entartet und Suchoperationen sind unnötig langsam. Hier würde eine Reihe von Rotationen die Situation verbessern. Ein AVL-Baum würde es allerdings nie soweit kommen lassen und hätte schon längst eingegriffen.

Da ein AVL-Baum Informationen über die Form des Baums speichert, müssen viele Operationen gegenüber des einfachen Suchbaums angepasst werden. So verändern zum Beispiel Rotationen die Balance. Dem trägt der einfache Suchbaum aber nicht Rechnung.

2.1 Rotationen in einem AVL-Baum

Bei Rotationen in AVL-Bäumen müssen nicht nur die Knoten neu verbunden werden, sondern es müssen auch die Balancen neu angepasst werden. Die neuen Balancen werden mit Hilfe von Formeln bestimmt. Diese beruhen auf einer rein mathematischen Überlegung und haben mit Algorithmik nicht viel zu tun. Deswegen werde ich hier auch nur die Formeln nennen. Der Beweis, dass diese in jedem Fall das richtige Ergebnis liefern, befindet sich am Ende des Artikels.

Links-Rotation

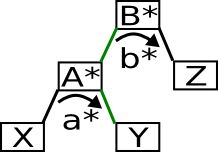
• a* = a - 1 - max(0, b)
• b* = b - 1 + min(0, a*)

Rechts-Rotation

• a* = a + 1 - min(0, b)
• b* = b + 1 + max(0, a*)

2.2 Wann rotieren?

Der Baum kann nur aus der Balance geraten, wenn wir einen Knoten anhängen oder abschneiden. Die Höhe wird bei diesen Operationen maximal um 1 verändert und somit auch die Balance. Da wir von einem ausbalancierten Baum ausgegangen sind, tauchen also schlimmsten Falls Balancen von -2 oder +2 auf. Wir brauchen daher gar keine Strategie um stärkere Entartungen zu behandeln, falls wir nach jeder solchen Operation den Baum wieder ins Gleichgewicht bringen.

Des Weiteren verändert das Einfügen oder Löschen nur die Balance der Elternknoten. Also können wir den Baum von unten nach oben ausbalancieren. Durch diese Vorgehensweise können wir sicher sein, dass Rotationen nur auf Knoten ausgeführt werden, die ausbalancierte Kinder haben.

2.3 Ausbalancieren

Wenn wir den Baum nach einer Veränderung nach oben durchwandern, um ihn zu reparieren, werden wir unweigerlich auf Balancen von -2 oder 2 stoßen. Diese wollen behandelt werden und dies kann man mit einer oder mehreren Rotationen anstellen. Auch hier ist es nicht direkt offensichtlich warum dies funktioniert. Bewiesen wird dies am Ende des Artikels.

Neben der eigentlichen Folge der Rotationen interessiert uns auch, um wie viel der Baum durch die Rotationen gekürzt wurde, da dies wiederum die Balance der höheren Knoten beeinflussen kann. Eine Verlängerung kommt nie vor.

Es gibt zwei Arten eines entarteten Knoten: Entweder er hat eine Balance von -2 oder eine von +2.

2.3.1 Knoten mit Balance -2

-2 bedeutet, dass der Baum linkslastig ist. Darum hängt die Vorgehensweise von der Balance des linken Kinds ab. Es gibt immer ein linkes Kind, da sonst die Balance nicht negativ sein könnte. Da der linke Unterbaum ausbalanciert ist, kann er drei Balancen besitzen.

Es gibt also 3 Unterfälle zu unterscheiden, welche von der Balance des Kindes abhängen.

• Es hat eine Balance von -1: Wir rotieren die Wurzel nach rechts. Dabei wird der Baum um eins gekürzt.
• Es hat eine Balance von 0: Wir rotieren die Wurzel nach rechts. Dabei wird die Höhe des Baums nicht verändert.
• Es hat eine Balance von +1: Wir rotieren zuerst das linke Kind der Wurzel nach links und anschließend die Wurzel nach rechts. Dabei wird der Baum um eins gekürzt.

2.3.2 Knoten mit Balance +2

Bei einem Knoten mit Balance +2 ist die Behandlung ähnlich, jedoch hängt die Therapie vom rechten Kind ab. Es gibt wieder drei Unterfälle:

• Es hat eine Balance von -1: Wir rotieren zuerst das rechte Kind der Wurzel nach rechts und anschließend die Wurzel nach links. Dabei wird der Baum um eins gekürzt.
• Es hat eine Balance von 0: Wir rotieren die Wurzel nach links. Dabei wird die Höhe des Baums nicht verändert.
• Es hat eine Balance von +1: Wir rotieren die Wurzel nach links. Dabei wird der Baum um eins gekürzt.

Es folgen ein paar Beispiele für einen Knoten mit Balance +2. Falls das rechte Kind eine Balance von 1 hat, dann sieht das Ganze in etwa folgendermaßen aus:

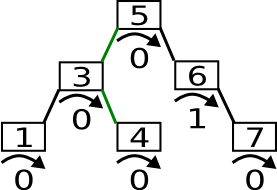
Für ein Kind mit Balance 0 ist ein Fall dem vorherigen sehr ähnlich ist, jedoch behält der Baum die gleiche Höhe.

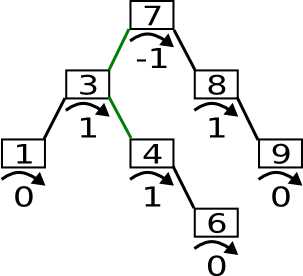
Der letzte Fall ist wahrscheinlich der eigenartigste. Viele Leser werden sich fragen, wieso man hier nicht einfach die Wurzel rotiert.
Ein Beispiel zeigt jedoch gut, dass man mit einer einfachen Links-Rotation der Wurzel nicht ans Ziel kommt.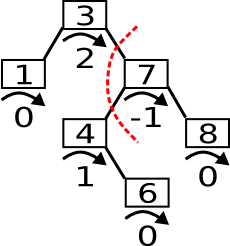

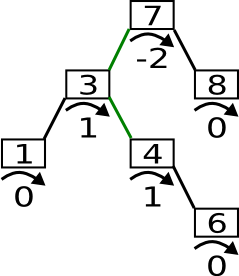
Die Lösung ist, zwei Rotationen auszuführen. Manchmal wird dieser Vorgang auch Doppelrotation genannt.

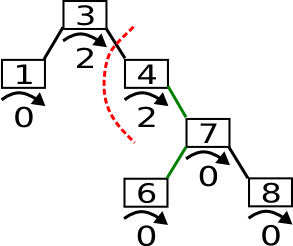
Es ist nicht schlimm, dass der eine Unterbaum nach der ersten Rotation aus der Balance gerät. Die zweite bügelt das wieder aus, und zwar immer. Wer es nicht glaubt, der soll sich den Beweis anschauen.

2.4 Gewicht anhängen

Wenn man einen Knoten einfügt, ohne die Balancen anzupassen, so wird er nicht beim balancieren berücksichtigt. Wenn man sich die Knoten als Balkenwaagen vorstellt, so besitzt der Knoten kein Gewicht. Deswegen müssen wir, nachdem sich der neue Knoten im Baum befindet, ihm ein Gewicht geben.

Um dies zu bewerkstelligen, laufen wir den Baum vom neuen Knoten aus bis zur Wurzel hoch. Die Balance der Knoten, denen wir unterwegs begegnen, müssen wir anpassen. Wenn wir von links kommen, so muss etwas von der Balance abgezogen werden. Falls von rechts, so muss etwas hinzugefügt werden.

In folgendem Fall muss etwas von der Balance abgezogen werden:

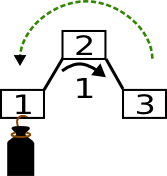
Wenn das Gewicht jedoch am anderen Kind hängt, so muss etwas dazu gerechnet werden:

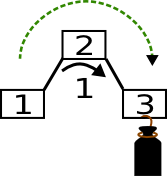
Als nächstes interessiert uns natürlich, wie schwer das Gewicht ist, das heißt, um wie viel wir die Balance verändern müssen. Da die Balance als Differenz der Höhen definiert ist, entspricht das Gewicht der Verlängerung des Unterbaums.

Der neue Knoten hat ein Gewicht von 1, da er an eine Stelle gekommen ist, an der sich kein Knoten befand, also der Unterbaum eine Höhe von 0 hatte. Der Unterbaum wurde also von 0 auf 1 erhöht, was einer Verlängerung, also einem Gewicht von 1 entspricht.

Mit diesem Wissen können wir den ersten Elternknoten verbessern, doch wie geht es weiter? Nun, wir müssen die Veränderung der Höhe, also das Gewicht des gerade behandelten Unterbaums bestimmen und dann den nächsten Elternknoten ausbessern.

Nicht immer wird die Höhe eines Unterbaums verändert, wenn wir ein Gewicht dranhängen, wie folgendes Beispiel zeigt:

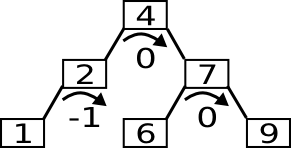
Die Höhe des gesamten Baum wird verändert, wenn man zum Beispiel an einen linkslastigen Baum ein Gewicht an das linke Kind hängt.

Falls das Gewicht an die selbe Seite kommt wie der Unterbaum, hinkt so wird er um dieses Gewicht verlängert. Dabei wird ein Baum mit Balance 0 als zu beiden Seiten hinkend angesehen.

Andernfalls hängt es davon ab, ob die Balance das Vorzeichen wechselt, also auf die andere Seite kippt. Wenn sie dies tut, dann entspricht das neue Gewicht dem Betrag der neuen Balance. Falls der Baum nicht kippt, so wird die Gesamthöhe nicht verändert. Ein Kippen kann nur durch Gewichte hervorgerufen werden, welche mindesten 2 wiegen.

Nachdem man nun das neue Gewicht ausgerechnet hat, muss man noch entartete Knoten bekämpfen. Der Grund warum wir überhaupt Balancen rechnen, war ja um zu wissen, wo und wie rotiert werden muss. Falls die neue Balance der Knoten +2 oder -2 entspricht so müssen wir eingreifen. Da dies die Höhe des Baum kürzen kann, kann es auch sein Gewicht veringern.

Nun wo der erste Elternknoten angepasst wurde, können wir mit der gleichen Methode alle weiteren anpassen.

Manche Leser werden wahrscheinlich Bedenken bei dieser Methode haben und sich fragen, ob es nicht möglich sei, dass die Variation der Höhen, welche durch das ursprüngliche Löschen oder Einfügen entstanden sind, sich mit denen, die durch das Ausbalancieren hervorgerufen werden, auftürmen und dadurch Knoten mit Balancen von -3 oder +3 entstehen. Diese Leser kann ich beruhigen, beide Veränderungen der Höhe wirken immer entgegengesetzt, falls sie sich überhaupt beeinflussen. Sie löschen sich also höchstens aus, wodurch wir nicht einmal bis zur Wurzel des Suchbaums hinauf wandern müssen.

2.5 Einfügen

Wie man einen Knoten einfügt, wurde bereits im vorherigen Kapitel besprochen. Man fügt den Knoten wie gewohnt an und hängt dann das Gewicht 1 an.

Die Komplexität ist logarithmisch, da wir den Baum im schlimmsten Fall einmal von oben nach unten und dann wieder nach oben durchlaufen und die Höhe logarithmisch von der Gesamtanzahl der Elemente abhängt.

2.6 Löschen

Um einen Knoten zu löschen, gehen wir ähnlich vor, wie beim einfachen Binär-Baum. Um ein Blatt oder einen Knoten mit nur einem Kind zu löschen, hängen wir zuerst ein Gewicht an, welches -1 wiegt, danach wird der Knoten wie gewohnt gelöscht.

Falls der Knoten zwei Kinder hat, so wird der Knoten zuerst getauscht, dann das Gewicht dran gehängt und anschließend wie ein Blatt gelöscht.

Da das Anhängen von Gewichten unter Umständen Rotationen mit sich zieht, ist es nicht offensichtlich, dass ein Blatt auch ein Blatt bleibt, nachdem das Gewicht daran hängt. Da das Gewicht negativ ist, werden die Elternknoten höchstens zu sehr zur anderen Seite des Baums hinhinken. Eine Rotation verändert aber nur Knoten, welche sich auf derselben Seite befinden, zu der der Baum hinhinkt. Zur Erinnerung wird bei einer Balance von +2 höchstens das rechte Kind und bei einer Balance von -2 höchstens das linke Kind verändert. Das Blatt, das wir löschen wollen, nimmt also nie an einer Rotation teil. Es bleibt also ein Blatt. Das gleiche gilt für Knoten mit nur einem Kind.

2.7 Andere Operationen

Sämtliche anderen Operationen in einem AVL-Baum entsprechen denen aus dem einfachen Suchbaum, so zum Beispiel das Durchwandern oder das Suchen. Manche sind sehr leicht abgeändert, wie zum Beispiel das Austauschen: Es müssen auch die Balancen ausgetauscht werden.

3 Implementierung

Da ein AVL-Baum an sich nur ein erweiterter Suchbaum ist, werde ich den Code aus dem vorherigen Artikel als Ausgangsbasis wiederverwenden. Ich werde nur auf Funktionen eingehen, die neu sind oder nicht trivial verändert wurden.

3.1 Darstellung

Die Knoten-Struktur erhält ein neues Mitglied und sieht nun folgendermaßen aus.

struct Node{
	Node*parent, *left, *right;
	T value;
	int balance;

	explicit Node(const T&value):
		parent(0), left(0), right(0), value(value), balance(0){}
};

3.2 Dump

Die Ausgabefunktion des Baumes muss nicht verändert werden, da sie immer noch funktioniert. Es könnte allerdings interessant sein, zusätzlich die Balancen der Knoten angezeigt zu bekommen. Dies kann durch eine Anpassung von format_label erreicht werden.

static std::string format_label(const Node*node){
	if(node){
		std::ostringstream out;
		out<<node->value<<'['<<node->balance<<']';
		return out.str();
	}else
		return "";
}

3.3 Debug-Checks

Ein AVL-Baum ist ein gutes Stück komplexer als ein einfacher Suchbaum und daher reicht es nicht mehr, nur am Ende jeder frei zugänglichen Methode zu überprüfen, ob der Baum so überhaupt richtig sein kann. Man muss Funktionen einführen, die testen, ob der Baum teilweise richtig ist. So ist es zum Beispiel möglich, dass sämtliche Zeiger richtig sind, jedoch die Balancen falsch ausgerechnet wurden. Darum breche ich is_wellformed in mehere Funktionen auf, welche alle nur einen Teil testen, also entweder die Zeiger oder die Balancen testen.

Dies ist sehr hilfreich bei der Fehlersuche, da man verhindert, dass Fehler verschleppt werden. Würde man nur am Ende jeder Operation testen, so könnte es sein, dass ein Test wegen einer falschen Balance fehlschlägt, obwohl der Code, der die Balance bestimmt, fehlerfrei ist. Wenn die Zeiger des Baums nicht mehr stimmen, so ist es gut möglich, dass richtiger Code daraus keinen gesunden Baum mehr formen kann. Der Fehler würde sich allerdings erst ganz am Ende bemerkbar machen, würde also bis zum Ende verschleppt, und dadurch weiß man nicht wirklich wo er sich befindet. Dadurch, dass man is_wellformed aufbricht, geht man dem aus dem Weg. Bevor man sich den Balancen zuwendet, kontrolliert man zuerst die Zeiger. Dadurch weiß man, dass, wenn ein Test fehlschlägt, welcher Balancen überprüft, der Fehler sich höchstwahrscheinlich im entsprechenden Code versteckt.

bool is_binary_tree(Node*node){
	if(node == 0)
		return true;
	if(*get_parent_ptr(node) != node)
		return false;
	if(!is_binary_tree(node->left))
		return false;
	if(!is_binary_tree(node->right))
		return false;
	return true;
}

Die Funktion is_binary_tree testet, ob die Zeiger im Baum stimmen.

bool is_avl_tree(Node*node){
	if(node == 0)
		return true;
	else if(
		static_cast<int>(get_height(node->right)) - static_cast<int>(get_height(node->left)) 
			!= node->balance)
		return false;
	else if(!is_avl_tree(node->right))
		return false;
	else if(!is_avl_tree(node->left))
		return false;
	return true;
}

is_avl_tree stellt fest, ob alle Balancen der Differenz der Höhen der Unterbäumen entsprechen.

bool is_balanced(Node*node){
	if(node == 0)
		return true;
	else if(node->balance < -1)
		return false;
	else if(1 < node->balance)
		return false;
	else if(!is_balanced(node->right))
		return false;
	else if(!is_balanced(node->left))
		return false;
	return true;
}

is_balanced überprüft, ob der Baum ausbalanciert ist.

bool is_wellformed(Node*node){
	if(!is_binary_tree(node))
		return false;
	if(!is_avl_tree(node))
		return false;
	if(!is_balanced(node))
		return false;
	return true;
}

Die is_wellformed-Funktion überprüft alles. Sie kommt vor allem am Ende von frei zugänglichen Methoden zum Einsatz. Der Test dürfte oft redundant sein, da alles bereits in der Mitte der Funktion durch die mehr spezialisierten Test überprüft wurde. Lieber aber einmal zu oft testen, als einmal zu wenig.

3.4 Kopierkonstruktor

Beim Kopierkonstruktor kopiert man einfach noch die Balancen von einem Baum in den anderen. Da sie genau die gleiche Form haben, unterscheiden sich die Balancen auch nicht. Während des Kopiervorgangs stimmen die Balancen jedoch nicht im unfertigen Baum, darum dürfen wir da nicht mehr mit is_wellformed den Zustand testen, sondern müssen auf is_binary_tree zurückgreifen. Die Grundidee des Kopiekonstruktor wird aber nicht verändert.

3.5 Rotationen

Die Implementierung der Rotationsfunktionen wird um die beiden Formeln erweitert, sie werden angewandt, nachdem die Knoten neu verbunden sind. Die Funktionen werden also um folgende Zeilen erweitert.

Node*rotate_left(Node*A){
	/* ... */

	A->balance = A->balance - 1 - std::max(0, B->balance);
	B->balance = B->balance - 1 + std::min(0, A->balance);

	return B;
}

Node*rotate_right(Node*A){
	/* ... */

	A->balance = A->balance + 1 - std::min(0, B->balance);
	B->balance = B->balance + 1 + std::max(0, A->balance);

	return B;
}

3.6 Ausbalancieren

Die Funktion zum Ausbalancieren entspricht einer if-else-Kette, welche die gleiche Fallunterscheidung wie in der Theorie vornimmt. Sie gibt zurück, um wie viel der Baum gekürzt wurde.

int balance(Node*&root){
	if(root->balance == 2){
		Node*child = root->right;
		if(child->balance == 1){
			root = rotate_left(root);
			return 1;
		}else if(child->balance == 0){
			root = rotate_left(root);
			return 0;
		}else if(child->balance == -1){
			rotate_right(child);
			root = rotate_left(root);
			return 1;
		}
	}else if(root->balance == -2){
		Node*child = root->left;
		if(child->balance == 1){
			rotate_left(child);
			root = rotate_right(root);
			return 1;
		}else if(child->balance == 0){
			root = rotate_right(root);
			return 0;
		}else if(child->balance == -1){
			root = rotate_right(root);
			return 1;
		}
	}else if(root->balance >= -1 && root->balance <= 1)
		return 0;
	assert(false);
}

3.7 Gewicht

Die Funktion zum Gewichtanhängen entspricht auch dem Verfahren, welches in der Theorie vorgestellt wurde. Obwohl sie recht kurz ist, dürfte es sich um die komplizierteste Funktion in diesem Artikel handeln. Es ist sehr einfach, bei ihrer Implementierung einen Fehler zu machen.

void add_weight(Node*now, int weigth){
	while(now != root && weigth != 0){		
		if(is_left_child(now)){
			now = now->parent;

			now->balance -= weigth;
			if(now->balance <= 0)
				weigth = std::min(weigth, -now->balance);
			else
				weigth = 0;
			weigth -= balance(now);
		}else{
			now = now->parent;

			now->balance += weigth;
			if(now->balance >= 0)
				weigth = std::min(weigth, now->balance);
			else
				weigth = 0;
			weigth -= balance(now);

		}
	}
}

3.8 Einfügen

Die Funktion zum Einfügen wird am Ende verändert, damit sie noch zusätzlich ein Gewicht anhängt.

bool insert(const T&value){
	/* ... */

	assert(is_binary_tree(root));
	add_weight(new_node, 1);
	assert(is_wellformed(root));
	return true;
}

3.9 Löschen

Die Löschmethode wird ähnlich wie die Funktion zum Einfügen modifiziert. Sie sieht nun folgendermaßen aus:

void remove(Node*node){
	// Ein Blatt
	if(!node->left && !node->right){
		add_weight(node, -1);
		*get_parent_ptr(node) = 0;
		delete node;
	}
	// Nur ein Kind
	else if(node->left && !node->right){
		add_weight(node, -1);
		*get_parent_ptr(node) = node->left;
		node->left->parent = node->parent;
		delete node;
	}else if(!node->left && node->right){
		add_weight(node, -1);
		*get_parent_ptr(node) = node->right;
		node->right->parent = node->parent;
		delete node;
	}
	// Zwei Kinder
	else{
		Node*other = get_prev_node(node);
		swap_nodes(node, other);

		remove(node);
	}
	assert(is_wellformed(root));
}

3.10 Andere Operationen

Die anderen Operationen wurden gar nicht oder nur sehr leicht verändert. Falls sie anders sind, so ist die Änderung banal und evident.

3.11 Experimentierkonsole

Auch die Experimentierkonsole wurde angepasst und lässt nun tiefe Einblicke in das Leben eines AVL-Baums zu.

Download-Link

4 Quellen

Folgende Links waren bei der Erstellung dieses Artikels sehr hilfreich:

• http://www.cmcrossroads.com/bradapp/ftp/src/libs/C++/AvlTrees.html
• http://de.wikipedia.org/wiki/AVL-Baum

Die Bilder wurden mit Inkscape erstellt.

5 Beweise

Es folgen die Beweise für die in der Implementierung benutzten Formeln.

5.1 Allgemeine Formeln

In folgenden Beweisen werde ich 2 Hilfsfunktionen min(a, b) und max(a, b) verwenden. Sie geben jeweils den kleineren Wert von a und b zurück.

Folgende Formeln sollten dem Leser bekannt sein:

• max(a, b) + c = max(a + c, b + c)
• max(a, b) - a = max(a - a, b - a) = max(0, a - b)
• -max(u, v) = min(-u, -v)

5.2 Notation

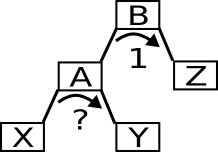
Mit h(R) ist die Höhe eines Unterbaums mit der Wurzel R gemeint.

Falls eine Operation den Baum verändert, so werden die Werte davor ohne Sternchen notiert und danach mit. Also h(X) ist die Höhe vor der Operation und h(X*) danach.

Wenn sich auf einer Grafik keine Angaben zu der Balance befinden, so ist irgendein ausbalancierter Unterbaum gemeint oder auch gar kein Unterbaum. Falls die Balance als ? angegeben wird, dann kann sie entweder nicht genau bestimmt werden oder ihr Wert interessiert uns nicht.

Buchstaben die vorne im Alphabet vorkommen, stehen für einen bestimmten Knoten und die, die hinten im Alphabet vorkommen, für irgendeinen ausbalancierten Unterbaum.

5.3 Rotationsformeln

Da Rechts- und Links-Rotationen symmetrisch sind, werde ich nur auf die Links-Rotation eingehen. Um die Formeln aufzustellen, geben ich allen Knoten und Balancen erst einmal Namen.

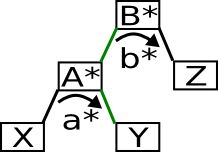
Da die Unterbäume der Knoten X, Y und Z nicht verändert werden, ändert sich ihre Balance auch nicht. Es müssen also nur die Balancen von A* und B* bestimmt werden. a und b sind bekannt und a* und b* werden gesucht.

Aus der Definition der Balancen können wir folgende Gleichungen ableiten:

• a = h(B) - h(X) (1)
• b = h(Z) - h(Y) (2)
• a* = h(Y) - h(X) (3)
• b* = h(Z) - h(A*) (4)

Über die Höhen von A* und B wissen wir folgendes:

• h(A*) = max(h(Y), h(X)) + 1 (5)
• h(B) = max(h(Y), h(Z)) + 1 (6)

(2) - (1) ergibt:

• b - a = h(Z) - h(Y) - h(B) + h(X)
• h(Y) - h(X) = - h(B) + h(Z) - b + a
• a* = - max(h(Y), h(Z)) - 1 + h(Z) - b + a | durch (5) und (3)
• a* = min(-h(Y), -h(Z)) - 1 + h(Z) - b + a
• a* = min(h(Z)-h(Y), 0) - 1 - b + a
• a* = min(b, 0) - 1 - b + a | durch (2)
• a* = a - 1 - max(0, b) (7)

(7) gibt uns eine Formel um a* zu bestimmen.

• h(Z) - h(A*) = h(Z) - h(A*) - b + b
• b* = h(Z) - h(A*) - h(Z) + h(Y) + b | durch (2) und (4)
• b* = - h(A*) + h(Y) + b
• b* = - max(h(Y), h(X)) - 1 + h(Y) + b | durch (3)
• b* = min(-h(Y), -h(X)) - 1 + h(Y) + b
• b* = min(0, h(Y) - h(X)) - 1 + b
• b* = min(0, a*) - 1 + b | durch (3)
• b* = b - 1 + min(0, a*) (8)

(8) gibt uns eine Formel um b* zu berechnen.

5.4 Ausbalancieren

Da die Methoden, um einen Knoten mit einer Balance von -2 oder +2 zu behandeln, nur spiegelverkehrt sind, werde ich nur den Fall +2 beschreiben. Wie bereits gesagt gibt es 3 Unterfälle.

5.4.1 Das Kind hat eine Balance von +1

Per Definition der Balance wissen wir, dass:

• h(Z) - h(Y) = 1 also h(Y) = h(Z) - 1 (1)
• h(B) - h(X) = 2 also h(X) = h(B) - 2 (2)

Aus (1) können wir schließen, dass h(Z) > h(Y) und daraus:

• h(B) = h(Z) + 1 (3)

(3) in (2) gibt uns einen Wert für h(X):

• h(X) = h(Z) + 1 - 2 = h(Z) - 1 (4)

Nach einer Links-Rotation sieht unser Baum wie folgt aus:

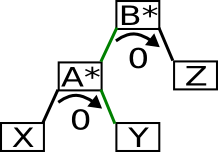
Aus (4) und (3) ergibt sich h(X) = h(Y) also ist

• Die Balance von A* : h(X) - h(Y) = 0
• h(A) = h(X) + 1 = h(Z) - 1 + 1 = h(Z) (5)

Aus (5) ergibt sich, die neue Balance von B:

• Die Balance von B* : h(A) - h(Z) = 0

Da alle Knoten eine Balance von 0 haben, ist der Baum im Gleichgewicht.

Errechnen wir die Anfangshöhe des Baums.

• h(A) = max(h(X)+1, h(B)+1)
• h(A) = max(h(X)+1, max(h(Y)+1, h(Z)+1)+1)
• h(A) = max(h(X)+1, h(Y)+2, h(Z)+2)
• h(A) = max(h(Z), h(Z)+1, h(Z)+2) | durch (1) und (4)
• h(A) = h(Z)+2

Nun die Endhöhe des Baums.

• h(B*) = max(h(A*)+1, h(Z)+1)
• h(B*) = max(max(h(X)+1, h(Y)+1)+1, h(Z)+1)
• h(B*) = max(h(X)+2, h(Y)+2, h(Z)+1)
• h(B*) = max(h(Z)+1, h(Z)+1, h(Z)+1) | durch (1) und (4)
• h(B*) = h(Z) + 1

Da h(A) - h(B*) = 1 wurde der Baum um 1 in der Höhe gekürzt.

5.4.2 Das Kind hat eine Balance von 0

Durch eine ähnliche Überlegung wie oben kommen wir auf folgende Gleichungen:

• h(X) = h(Z)-1 (1)
• h(Y) = h(Z) (2)

Daraus folgt folgende Rotation:

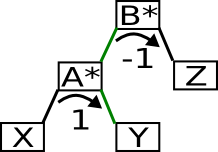
Die Rotation bringt den Baum also ins Gleichgewicht.

Errechnen wir die Anfangshöhe des Baums.

• h(A) = max(h(X)+1, h(Y)+2, h(Z)+2)
• h(A) = max(h(Z)+2, h(Z)+2, h(Z)+2) | durch (1) und (2)
• h(A) = h(Z) + 2

Nun die Endhöhe des Baums.

• h(B*) = max(h(X)+2, h(Y)+2, h(Z)+1)
• h(B*) = max(h(Z)+1, h(Z)+2, h(Z)+1) | durch (1) und (2)
• h(B*) = h(Z) + 2

Da h(A) - h(B*) = 0 wurde der Baum nicht in der Höhe geändert.

5.4.3 Das Kind hat eine Balance von -1

In diesem Fall führt eine einfache Links-Rotation nicht zum Ziel. Als erstes muss das rechte Kind rechts rotiert werden und anschließend erst die Wurzel nach links.

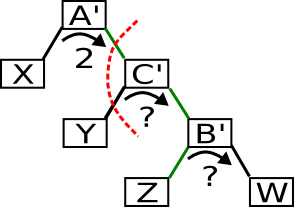
Die Berechung der Balancen ist hier schwieriger. Als erstes definieren wir M = max(h(Y), h(Z)). Da der Unterbaum in C im Gleichgewicht ist, wissen wir:

• M - h(Y) = 0 oder 1
• M - h(Z) = 0 oder 1

Analog zu der Vorgehensweise bei den zwei bereits genannten Fällen können wir sagen, dass:

• h(C) = M + 1
• h(B) = M + 2
• h(W) = M
• h(X) = M

Die neue Balance von A und B kann wie folgt eingegrenzt werden:

• h(Y) - h(X) = h(Y) - M = -(0 oder 1) = 0 oder -1
• h(W) - h(Z) = M - h(Z) = 0 oder 1

Es ist also egal, was die Ausgangsbalance von C ist, die neue Balancen von A und B sind immer im Zielbereich.

Die neue Balance von C kann auch eingeschränkt werden:

• h(B*) - h(A*) = [h(W) - h(Z)] - [h(Y) - h(X)] = M - h(Z) - h(Y) + M = [M - h(Y)] + [M - h(Z)] = (0 oder 1) + (0 oder 1) = 0 oder 1 oder 2

Für den Fall 2 müssten aber sowohl M - h(Y) = 1 und M - h(Z) = 1, was aber nicht möglich ist, da in diesem Fall M größer wäre, als das Maximum von h(Y) und h(Z). Der Baum ist also in der Balance.

Die Anfangshöhe kann wie folgt berechnet werden:

• h(A) = max(h(X) + 1, h(B) + 1)
• h(A) = max(h(X) + 1, h(C) + 2, h(W) + 2)
• h(A) = max(M + 1, M + 3, M + 2)
• h(A) = M + 3

Und die Endhöhe folgendermaßen:

• h(C*) = max(h(A*)+1, h(B*)+1)
• h(C*) = max(h(X)+2, h(Y)+2, h(Z)+2, h(W)+2)
• h(C*) = max(h(X), h(Y), h(Z), h(W))+2
• h(C*) = max(h(X), max(h(Y), h(Z)), h(W))+2
• h(C*) = max(M, M, M)+2
• h(C*) = M+2

Da h(A) = h(C*) + 1 wurde die Höhe des Baums um 1 gekürzt.

[Markus300]

Hey super Artikel sowas habe ich gesucht! danke

[andre111]

hab nach dem binären suchbaum sofort hier weiter gemacht, ganz großes lob meinerseits, echt gut gelungen

[JensX]

Klasse
Der Unterschied zwischen einem "normalen" binären Suchbaum und einem "voll" ausbalancierten ist gravierend.
Der Test mit 100000 Datensätzen beträgt bei mir 8 min zu 9 Sek.
Danke für die TOP-Beschreibung.

[Nick Lehmann]

Das ist echt ein klasse Tutorial. Es hat mir sehr viel für meine eigene noch laufende Implementation in Perl geholfen.
Allerdings gibt es einen kleinen Fehler. Im zweiten Abschnitt wird über Höhen und Balancen geschrieben. Im Gegensatz zum Text ziehst du die linke Höhe von der rechten ab. Aber ansonsten wunderbar

[MaximGast]

einfach klasse danke