[X] Binary Heaps
-
Binary Heaps
Heaps sind eine Datenstruktur, die vor allem bei der Implementierung von Priority-Queues verwendet wird. Die hier vorgestellte Datenstruktur hat nichts mit der Speicherverwaltung von C++ zu tun.
In erster Linie möchte ich binary Heaps vorstellen und zeigen, wie man sie in C++ effizient implementiert. Die Implementierung wird dabei nicht unbedingt mit der, wie sie in klassischen Algorithmenbüchern beschrieben ist, übereinstimmen. Ein Blick dorthinein lohnt sich auf jeden Fall trotzdem noch, um zum Einen eine andere Darstellung zu sehen, und vielleicht auch die klassische Implementierung kennen zu lernen.
Nebenbei wird Heap-Sort, ein Sortierverfahren, das stets mit höchstens 2N*logN Element-Vergleichen sortiert, abfallen. Außerdem wird noch kurz auf die Unterstützung in C++ durch die STL eingehen.1 Heaps - Die Theorie
Zur einfacheren Darstellung treffen wir zunächst eine vereinfachende Annahme, nämlich dass alle Schlüssel ganze Zahlen sind. Letztlich benötigen wir aber nur die Möglichkeit zu vergleichen.
Ein einfacher Heap bietet nach außen nur drei Operationen an:
- getMin, gibt das kleinste Elemente im Heap zurück.
- insert, fügt einen neuen Knoten in den Heap ein.
- deleteMin, löscht den Knoten mit dem kleinsten Schlüssel aus dem Heap.
getMin hat eine Laufzeit von O(1), alle anderen Operationen haben bei der hier vorgestellten Implementierung eine worst-case Laufzeit von O(log n). Insert hat im Schnitt sogar konstante Laufzeit.
Ein binary Heap ist ein Binärbaum, der zusätzlich folgende Eigenschaften erfüllt:
H1) Er ist soweit wie möglich balanciert, nur die letzte Schicht darf nicht voll besetzt sein. Die letzte Schicht muß linksbündig ausgefüllt sein.
H2) Für jeden Knoten gilt: sein Schlüssel ist kleiner als die Schlüssel seiner Kinder.
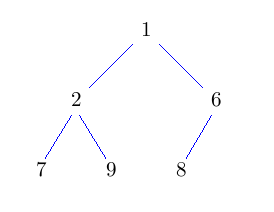
Eigenschaft H1) wird uns später eine sehr effiziente Implementierung der Baumstruktur erlauben, Eigenschaft H2) garantiert, dass die Operationen wie deleteMin effizient ausgeführt werden können.
Die Reihenfolge der Kinder eines Knotens ist dagegen beliebig und nicht wie bei einem Suchbaum geordnet. Das linke Kind muss nicht das kleinere sein.Kommen wir nun zu den 3 Operationen.
1.1 getMin
Das ist einfach. Aufgrund der Eigenschaft H2) muß die Wurzel der Knoten mit dem keinsten Schlüssel sein. Wir können also einfach die Wurzel zurückgeben. Das geht in konstanter Zeit.
1.2 insert
Die insert-Operation ist schon schwieriger. Wir gehen davon aus, dass wir zu Beginn einen korrekten Heap haben.
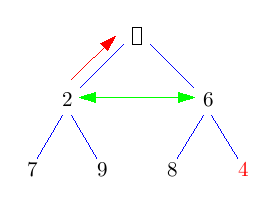
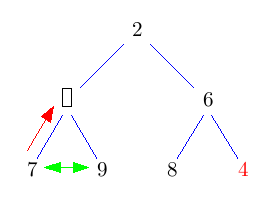
Beim Einfügen wird der neue Knoten einfach dort eingehängt, wo der nächste Knoten hin muss: In der untersten Ebene soweit links, wie möglich. Damit ist Eigenschaft H1) erfüllt. Leider ist Eigenschaft H2) noch nicht erfüllt.Um den Heap zu "reparieren" vertauschen wir den neu eingefügten Knoten so lange mit seinem Vater, bis die Eigenschaft erfüllt ist.
Im Pseudo-Code sieht das so aus:solange Schlüssel kleiner als der des Vaterknotens: Vertausche Knoten mit seinem VaterDieses nach oben durchsickern des Knotens heißt auch "sift-up".
Die grünen <-> Pfeile symbolisieren in den folgenden Bildern einen Vergleich, rote Pfeile/Doppelpfeile symbolisieren ein move/swap.
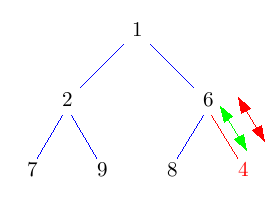
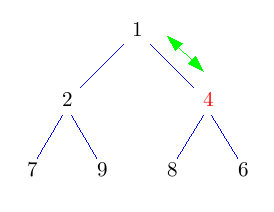
Das Auffinden der richtigen Stelle geht in konstanter Zeit (wie werden wir in der Implementierung sehen). Der gesamte Baum hat Höhe log N, daher kann auch sift-up höchstens log N Schritte brauchen. Im Schnitt sind sogar nur O(1) sift-up Schritte pro Einfügung nötig.
1.3 deleteMin
Im Prinzip müssen wir an dieser Stelle nur die Wurzel des Baumes löschen. Allerdings müssen wir die Datenstruktur anschließend noch wieder reparieren.
An dieser Operation scheiden sich ein bißchen die Geister. Die meisten Lehrbücher, zum Beispiel Sedgewick schlagen folgendes Vorgehen vor:
Entferne die Wurzel und setze an dessen Stelle das Knoten, das am weitesten unten rechts im Baum steht. Dadurch erhalten wir wieder einen Baum, der zumindest Eigenschaft H1) erfüllt. Nun lassen wir die neue Wurzel nach unten durchsickern, bis auch Eigenschaft H2) erfüllt ist. Solange sein Schlüssel nicht kleiner ist, als der seiner beiden Kinder, vertausche ihn mit dem Kind mit dem kleineren Schlüssel.
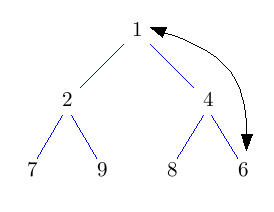
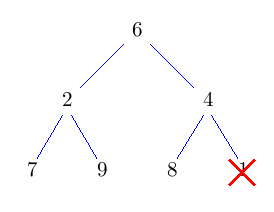
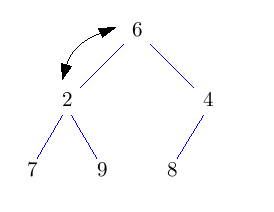
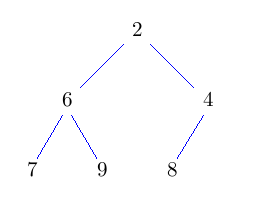
Dieses nach unten Durchsickern lassen des Knotens heißt auch sift-down. Das Vertauschen des Wurzelknotens mit dem Knoten am weitesten unten rechts, sowie das löschen des Wurzelknotens geht wieder in konstanter Zeit. Der neue Wurzelknoten kann höchstens bis nach ganz unten in den Baum durchsickern. Also hat deleteMin eine Laufzeit von O(log n).
Etwas unschön ist dabei der Vergleich mit beiden Kindern und der beiden Kinder nochmals untereinander. Man kann das zwar mit 2 Vergleichen hinbekommen, indem zunächst das kleinere Kind ermittelt und dann dieses mit dem Knoten, der durchsickern soll vergleicht, aber es gibt auch eine Alternative, die hier mit einem Vergleich auskommt.
1.3 deleteMin - Alternative
Hier soll nun eine andere Implementierung von deleteMin vorgestellt werden, die diesen Makel beseitigt und dadurch etwas schneller sein könnte. Dieses "schneller" ist allerdings mit Vorsicht zu genießen. Auf meinem Rechner ist diese Implementierung für große Datenmengen etwas schneller als die STL-Implementierung.
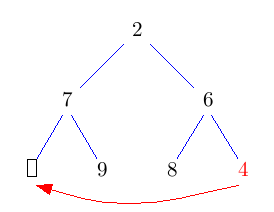
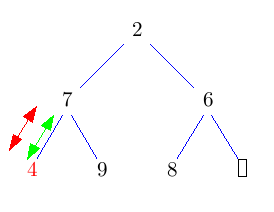
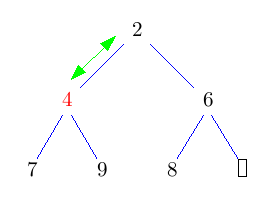
Die Idee ist, die Wurzel einfach rauszulöschen und das entstehende Loch nach unten durchsickern zu lassen, indem man immer das kleinere Kind nach oben zieht. Das kostet jeweils nur einen Vergleich. Dadurch landet das Loch nach log(n) Schritten in der untersten Ebene. Nun können wir es mit dem Blatt ganz rechts unten im Baum vertauschen und das Loch endlich wegfallen lassen. Nun müssen wir nur noch den getauschten Knoten wieder nach oben durchsickern lassen. Das geht aber im Schnitt sogar in konstanter Zeit.
Im folgenden Bild bedeuten grüne Doppelpfeile einen Vergleich, rote Pfeile move und rote Doppelpfeile swap.
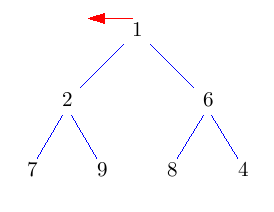
2 Anwendungen
Nachdem nun geklärt ist, was Heaps eigentlich sind und wie sie funktionieren, möchte ich, bevor wir zur Implementierung kommen, noch kurz zwei kleine Anwendungen von Heaps besprechen.
2.1 Priority Queues
Zum Einen werden Heaps verwendet um Priority-Queues zu implementieren. Man baut sich einfach einen Heap mit allen in der Queue befindlichen Elementen auf. Wird das nächste Elemente angefordert, führt man einfach deleteMin aus und gibt das kleinste Element zurück. Das Einfügen in die Queue ist ein simples Einfügen in den Heap.
template <typename T> class PriorityQueue { public: T deleteMin() { T item = heap_.getMin(); heap_.deleteMin(); return item; } void insert(T const& item) { heap_.insert(item); } private: Heap<T> heap_; }Ausgefeiltere Implementieren lassen vielleicht auch noch die Angabe eines Vergleichsoperators zu.
Möchte man allerdings auch Dinge, wie das Löschen von Elementen oder das Verändern von Prioritäten (also Schlüsseln im Heap) unterstützen wird die Sache etwas kniffliger und läßt sich auch nicht mehr ganz so effizient implementieren. Die Performance-Garantien im O-Kalkül können aber eingehalten werden. Mit noch etwas Mehraufwand läßt sich sogar die join-Operation, also die Vereinigung zweier Warteschlangen zu einer großen effizient implementieren. Aber dazu wird es vielleicht irgendwann mal einen eigenen Artikel geben.
2.2 Heapsort
Wie kann man nun mit Heaps sortieren? Auch das ist recht naheliegend.
Man fügt alle Elemente, die man sortieren möchte in den Heap ein und holt sie nacheinander mit deleteMin wieder heraus.Das sind n Insert-Operationen und n delete-Min-Operationen. Beide Einzeloperationen haben jeweils eine Laufzeit von O(log n). Heapsort hat also eine Laufzeit von O(n log n) und gehört damit zu den effizienten Sortierverfahren. Es benötigt immer, auch im worst-case maximal 2n log n Vergleiche.
3 Implementierung
So, nun kommen wir zum spannenden Teil. Wie implementiert man sowas effizient? Den Baum wirklich als Baum mit Parent- und Childpointern abzuspeichern wäre ziemlich ineffizient. Durch den strikten Aufbau des Baumes kann man ihn allerdings sehr einfach in einem Array abspeichern.
Dazu schauen wir uns noch einmal den Baum an und nummerieren die Knoten durch, in dem wir sie Zeile für Zeile jeweils von links nach rechts durchlaufen.
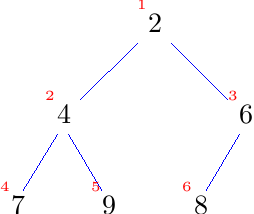
Nun legen wir den Baum in einem Array ab, indem wir jeden Knoten an den Index legen, der seiner Nummerierung entspricht.
Das sieht so aus:[ ?, 2, 4, 6, 7, 9, 8, ? ]Die Frage ist:
Warum beginnnen wir nicht, wie jeder gute Programmierer bei 0 zu zählen?
Außerdem liegen die Daten nun scheinbar willkürlich in dem Array. Wo ist unser schöner Baum geblieben?Man kann sich aber leicht klar machen, daß man anhand der Indizes sehr leicht immer noch im Baum navigieren kann.
Der Index des Vaterknotens von Knoten i ist einfach i/2.
Die Indizes der Kinderknoten von Knoten i sind 2*i und 2*i+1.
Da der Heap in der letzten Reihe von links nach rechts aufgefüllt wird, kann man durch Vergleich der errechneten Indizes mit der aktuellen Heap-Größe herausfinden, ob das Kind existiert.Vielleicht ist das auch ein guter Grund seine Arrays ab 1 zu nummerieren.

Alles was wir brauchen, um im Heap zu navigieren sind also Multiplikationen mit 2, Addition und Division durch 2, sowie einige Vergleiche. Das sind sehr einfache und schnelle Operationen, wir können also auf eine sehr schnelle Implementierung hoffen.
Mit der Platzverschwendung des ersten Elements (Index 0) können wir entweder leben, oder aber vor jedem Array-Zugriff vom errechneten Index noch 1 abziehen. Da wir aber so schnell wie möglich sein wollen verschwenden wir lieber etwas Platz. Zudem macht es die Implementierung etwas einfacher.Nachdem die Idee zur Implementation nun klar ist, können wir loslegen.
3.1 Der Rahmen
template<typename T, size_t MAX_SIZE> class Heap { public: Heap(); T getMin() const; void insert(T const& element); void deleteMin(); private: size_t getFather(size_t i) const { return i/2; } size_t getLeftChild(size_t i) const { return 2*i; } size_t getRightChild(size_t i) const { return 2*i + 1; } bool isRoot(size_t i) const { return i==1; } bool isLastElement(size_t i) const { return i==size_; } size_t getRoot() const { return 1; } bool compare(T const& lhs, T const& rhs) { return lhs < rhs; } T elements_[MAX_SIZE+1]; size_t size_; };Die father/child-Funktionen kapseln die Adressberechnungen, und machen so das Programm lesbarer.
Das ist zunächst mal alles was wir brauchen. Im Konstruktor initialisieren wir den Heap leer. Dazu müssen wir nur die Größe auf 0 setzen.3.2 Konstruktor
template<typename T, size_t MAX_SIZE> Heap::Heap() : size_(0) { }3.3 getMin
Auch getMin ist einfach:
template<typename T, size_t MAX_SIZE> T Heap::getMin() const { assert(size_ != 0); // je nach Geschmack könnte man auch if(...) throw out_of_range schreiben. return elements_[1]; }3.3 insert
So, nun kommen die härteren Brocken. Zur Erinnerung: Bei insert, fügen wir das neue Element in der untersten Zeile des Baums soweit links wie möglich ein und lassen es dann nach oben durchsickern.
template<typename T, size_t MAX_SIZE> void Heap::insert(T const& element) { size_t current = ++size_; size_t father = getFather(current); while(!isRoot(current) && compare(element, elements_[father])) { // Wir sind noch nicht an der Wurzel und unser Element ist "kleiner" als der Vater // also sickern wir nach oben elements_[current] = elements_[father]; current = father; father = getFather(current); } elements_[current] = element; }Eine mögliche Optimierung wäre die Platzierung eines Sentinels mit minimalem Key an Stelle 0 im Index. Dann könnte auf die Abfrage !isRoot verzichtet werden. Allerdings gibt es ein solches Element nicht für jeden Typ T.
3.4 deleteMin
Jetzt fehlt nur noch die deleteMin-Methode. Hier wird eine Implementierung der zweiten Variante vorgestellt. Zur Erinnerung: Wir löschen das kleinste Element und füllen die Lücke, indem wir immer das kleinere Kind nach oben ziehen. Anschließend tauschen wir die Lücke mit dem letzten Element des Heaps und lassen es nach oben sickern.
template<typename T, size_t MAX_SIZE> void Heap::deleteMin() { size_t current = getRoot(); size_t child = getLeftChild(current); if(child <= size_) { do { // wenn child nicht das letzte Element (der Knoten also 2 Kindet hat) // wechsle zum rechten Kind, wenn es kleiner ist child += (!isLastElement(child) && compare(elements_[child+1], elements_[child])); elements_[current] = elements_[child]; current = child; child = getLeftChild(current); } while(child <= size_); } // die Lücke ist nun unten angekommen // tausche mit letztem Blatt und vermindere Größe um 1. T element = elements_[size_--]; // jetzt noch das Blatt wieder hochsickern lassen. size_t father = getFather(current); while(!isRoot(current) && compare(element, elements_[father])) { elements_[current] = elements_[father]; current = father; father = getFather(current); } elements_[current] = element; }Damit ist auch die letzte Funktion geschafft.
3.5 Details zur Implementierung
Das war's zunächst mal von der Implementierungsseite. Durch die Kapselung der father/child/isRoot etc.-Funktionen könnte man nun auch leicht die Platzverschwendung bei Element 0 loswerden. father(i) = i/2 bleibt, leftchild(i) = (i+1)*2-1 usw. Allerdings muss man auch in den Funktionen einige Vergleiche mit size_ ändern. Ob und wieviel langsamer es danach ist, müsste man mal nachmessen. Dazu habe ich aber gerade keine Lust. Außerdem stört mich der kleine Platzoverhead nicht. Wir hatten ja sogar festgestellt, dass man ihn zum Beispiel als Sentinel nutzen könnte, indem man zum Beispiel bei einem Heap<unsigned int> eine 0 reinschreibt. Auch hier wäre eine Messung interessant, ob es die Performance steigert (laut meinen Messungen bringt es was). Ein heißer Kandidat für solche Messungen ist übrigens heap_sort, oder auch die Verwendung in einer Priority-Queue.
4 Heaps in der STL
Auch die STL bietet eine Implementierung der Datenstruktur Heap, und auch heap-sort ist vorhanden. Die Heaps aus der STL sind Max-Heaps, das heißt an der Wurzel steht das größte Element, nicht wie in unserer Implementierung das Kleinste. Das ist natürlich nur eine Frage des Sortierkriteriums.
Im Header <algorithm> sind folgende Funktionen:
void make_heap(RandomAccessIterator beg,RandomAccessIterator end);Baut in der Range einen Heap, indem es die Elemente so umsortiert, daß an der der Stelle beg das größte Element steht.
void push_heap(RandomAccessIterator beg, RandomAccessIterator end)Erwartet, daß die Range [beg, end-1) bereits ein heap ist und fügt diesem das Element an der Stelle end hinzu.
void pop_heap(RandomAccessIterator beg, RandomAccessIterator end)Erwartet, daß [big, end) ein Heap ist und nimmt das größte Element aus dem Heap heraus und legt es an der nun frei werdenden Stelle end ab.
sort_heap(RandomAccessIterator beg, RandomAccessIterator end)Erwartet, daß [beg, end) ein heap ist und wandelt diesen in eine sortierte Folge um. Danach ist die Sequenz kein Heap mehr!
Jede dieser Funktionen gibt es auch noch in einer weiteren Variante mit einem zusätzlichen Parameter um das Sortierkriterium festzulegen. Das folgende Codestück zeigt wie diese Funktionen verwendet werden. Dabei ist zu beachten, dass beim STL-Heap das größte Element Wurzel des Baums ist. Dies hat den Vorteil, dass nachdem alle Elemente aus dem Heap entfernt wurden, das Array direkt aufsteigend sortiert ist.
int data[10] = {11,5,14,12,3,4,9, 8, 20}; make_heap(data,data+9); // erstelle heap, der alle Elemente außer der 20 enhält cout << "groesstes Element: " << data[0] << "\n"; push_heap(data,data+10); // füge 20 hinzu cout << "Neues groesstes Element: " << data[0] << "\n"; cout << "Entferne alle Elemente aus dem Heap: "; for(size_t i=10; i>0;--i) { cout << data[0] << " "; pop_heap(data,data+i); } cout << "\nInhalt des Arrays am Ende: "; for(size_t i=0;i<10;++i) { cout << data[i] << " "; }5 Ausblick
In diesem Artikel wurde gezeigt, was ein binary Heap ist und wie man ihn implementiert. Es sind aber auch noch einige Dinge offen: Der hier vorgestellte Heap ist statisch. Wer ihn dynamisch wachseln lassen möchte, könnte als zugrundeliegende Datenstruktur einen std::vector benutzen. Interessant wäre es auch, das Array über einen Pointer zu adressieren und ähnlich wie die STL-Variante den Heap inplace in einem gegebenen Speicherbereich zu erzeugen. Diese Funktionalität könnte man über einen eigenen Konstruktor bereitstellen. Außerdem wäre es nett wenn man die Vergleichsfunktion mit angeben könnte. Durch die Verwendug der compare-Funktion für alle Elemente-Vergleiche sollte das kein Problem sein.
Interessant für eine flexiblere Priority Queue ist die Möglichkeit Elemente auch wieder zu löschen oder ihren Key zu verändern (vor allem verkleinern). Da es keine Möglichkeit gibt in einem Heap effizient zu suchen, müßte der Index des Knotens, der gelöscht werden soll bekannt sein. Dann könnte man ihn einfach mit dem letzten Blatt vertauschen, sodaß er gelöscht werden kann. Anschließend muß man reingetauschten Knoten noch nach unten durchsickern lassen. Möglicherweise wäre es dann interessant, doch eine Funktion siftdown(i) zu implementieren, die das übernimmt. Der Code ist im Prinzip vorhanden. Es ist klar, dass diese Operation in O(log n) Zeit läuft. Damit läßt sich auch das ändern eines Keys über remove/insert implementieren. Die Laufzeit ist ebenfalls O(log n) Zeit.
Es gibt noch weitere Heaps, man könnte zum Beispiel einen 4-ary Heap oder gar Bäume mit noch höherem Grad bauen. Da viele aktuelle Prozessorarchitekturen allerdings sehr wenig Register haben wird das nicht viel Effizienter als ein binary Heap. In Zukunft könnte das aber anders aussehen. Unterschiedliche Heap-Varianten bieten unterschiedliche Laufzeitgarantien. Für spezielle Anwendungen und wenn es auf Performance wirklich ankommt, lohnt sich also ein Blick auf http://de.wikipedia.org/wiki/Heap_%28Datenstruktur%29. Vielleicht wird es auch noch einen zweiten Teil dieses Artikels geben, in dem dann Pairing-Heaps und Fibonacci-Heaps vorgestellt werden.
6 Quellen
- http://de.wikipedia.org/wiki/Heap_%28Datenstruktur%29
- Algorithmen in C++, Robert Sedgewick, Addison-Wesley (1999)
- Vorlesungsfolien "Algorithm Engineering", Prof. Sanders, Uni KA(SS06)
- The C++ Standard Library, Nicolai M. Josuttis, Addison-Wesley (1999)
-
So, ich bin jetzt nochmal über den kompletten Text drüber. Der Code muss noch überarbeitet werden, das mache ich als nächstes. Danach nochmal komplett lesen und dann kommt's auf [R], oder wie war das richtige Kürzel?
-
Wenn die Tippfehler raus sollen, ist R richtig.
-
Binary Heaps
Heaps sind eine Datenstruktur, die vor allem bei der Implementierung von Priority-Queues verwendet wird. Die hier vorgestellte Datenstruktur hat nichts mit der Speicherverwaltung von C++ zu tun.
In erster Linie möchte ich binary Heaps vorstellen und zeigen, wie man sie in C++ effizient implementiert. Die Implementierung wird dabei nicht unbedingt mit der, wie sie in klassischen Algorithmenbüchern beschrieben ist, übereinstimmen. Ein Blick dorthinein lohnt sich auf jeden Fall trotzdem noch, um zum Einen eine andere Darstellung zu sehen, und vielleicht auch die klassische Implementierung kennen zu lernen.
Nebenbei wird Heap-Sort, ein Sortierverfahren, das stets mit höchstens 2N*logN Element-Vergleichen sortiert, abfallen. Außerdem wird noch kurz auf die Unterstützung in C++ durch die STL eingegangen.1 Heaps - Die Theorie
Zur einfacheren Darstellung treffen wir zunächst eine vereinfachende Annahme, nämlich dass alle Schlüssel ganze Zahlen sind. Letztlich benötigen wir aber nur die Möglichkeit zu vergleichen.
Ein einfacher Heap bietet nach außen nur drei Operationen an:
- getMin, gibt das kleinste Elemente im Heap zurück.
- insert, fügt einen neuen Knoten in den Heap ein.
- deleteMin, löscht den Knoten mit dem kleinsten Schlüssel aus dem Heap.
getMin hat eine Laufzeit von O(1), alle anderen Operationen haben bei der hier vorgestellten Implementierung eine worst-case Laufzeit von O(log n). Insert hat im Schnitt sogar konstante Laufzeit.
Ein binary Heap ist ein Binärbaum, der zusätzlich folgende Eigenschaften erfüllt:
H1) Er ist soweit wie möglich balanciert, nur die letzte Schicht darf nicht voll besetzt sein. Die letzte Schicht muss linksbündig ausgefüllt sein.
H2) Für jeden Knoten gilt: sein Schlüssel ist kleiner als die Schlüssel seiner Kinder.

Eigenschaft H1) wird uns später eine sehr effiziente Implementierung der Baumstruktur erlauben, Eigenschaft H2) garantiert, dass die Operationen wie deleteMin effizient ausgeführt werden können.
Die Reihenfolge der Kinder eines Knotens ist dagegen beliebig und nicht wie bei einem Suchbaum geordnet. Das linke Kind muss nicht das kleinere sein.Kommen wir nun zu den 3 Operationen.
1.1 getMin
Das ist einfach. Aufgrund der Eigenschaft H2) muss die Wurzel der Knoten mit dem kleinsten Schlüssel sein. Wir können also einfach die Wurzel zurückgeben. Das geht in konstanter Zeit.
1.2 insert
Die insert-Operation ist schon schwieriger. Wir gehen davon aus, dass wir zu Beginn einen korrekten Heap haben.
Beim Einfügen wird der neue Knoten einfach dort eingehängt, wo der nächste Knoten hin muss: In der untersten Ebene soweit links, wie möglich. Damit ist Eigenschaft H1) erfüllt. Leider ist Eigenschaft H2) noch nicht erfüllt.Um den Heap zu "reparieren" vertauschen wir den neu eingefügten Knoten so lange mit seinem Vater, bis die Eigenschaft erfüllt ist.
Im Pseudo-Code sieht das so aus:solange Schlüssel kleiner als der des Vaterknotens: Vertausche Knoten mit seinem VaterDieses nach oben Durchsickern des Knotens heißt auch "sift-up".
Die grünen <-> Pfeile symbolisieren in den folgenden Bildern einen Vergleich, rote Pfeile/Doppelpfeile symbolisieren ein move/swap.


Das Auffinden der richtigen Stelle geht in konstanter Zeit (wie, werden wir in der Implementierung sehen). Der gesamte Baum hat die Höhe log N, daher kann auch sift-up höchstens log N Schritte brauchen. Im Schnitt sind sogar nur O(1) sift-up Schritte pro Einfügung nötig.
1.3 deleteMin
Im Prinzip müssen wir an dieser Stelle nur die Wurzel des Baumes löschen. Allerdings müssen wir die Datenstruktur anschließend noch wieder reparieren.
An dieser Operation scheiden sich ein bisschen die Geister. Die meisten Lehrbücher, zum Beispiel Sedgewick, schlagen folgendes Vorgehen vor:
Entferne die Wurzel und setze an deren Stelle den Knoten, der am weitesten unten rechts im Baum steht. Dadurch erhalten wir wieder einen Baum, der zumindest Eigenschaft H1) erfüllt. Nun lassen wir die neue Wurzel nach unten durchsickern, bis auch Eigenschaft H2) erfüllt ist. Solange sein Schlüssel nicht kleiner ist, als der seiner beiden Kinder, vertausche ihn mit dem Kind mit dem kleineren Schlüssel.




Dieses nach unten Durchsickernlassen des Knotens heißt auch sift-down. Das Vertauschen des Wurzelknotens mit dem Knoten am weitesten unten rechts, sowie das Löschen des Wurzelknotens, geht wieder in konstanter Zeit. Der neue Wurzelknoten kann höchstens bis nach ganz unten in den Baum durchsickern. Also hat deleteMin eine Laufzeit von O(log n).
Etwas unschön ist dabei der Vergleich mit beiden Kindern und der beiden Kinder nochmals untereinander. Man kann das zwar mit 2 Vergleichen hinbekommen, indem zunächst das kleinere Kind ermittelt und dann dieses mit dem Knoten, der durchsickern soll vergleicht, aber es gibt auch eine Alternative, die hier mit einem Vergleich auskommt.
1.3 deleteMin - Alternative
Hier soll nun eine andere Implementierung von deleteMin vorgestellt werden, die diesen Makel beseitigt und dadurch etwas schneller sein könnte. Dieses "schneller" ist allerdings mit Vorsicht zu genießen. Auf meinem Rechner ist diese Implementierung für große Datenmengen etwas schneller als die STL-Implementierung.
Die Idee ist, die Wurzel einfach rauszulöschen und das entstehende Loch nach unten durchsickern zu lassen, indem man immer das kleinere Kind nach oben zieht. Das kostet jeweils nur einen Vergleich. Dadurch landet das Loch nach log(n) Schritten in der untersten Ebene. Nun können wir es mit dem Blatt ganz rechts unten im Baum vertauschen und das Loch endlich wegfallen lassen. Nun müssen wir nur noch den getauschten Knoten wieder nach oben durchsickern lassen. Das geht aber im Schnitt sogar in konstanter Zeit.
Im folgenden Bild bedeuten grüne Doppelpfeile einen Vergleich, rote Pfeile move und rote Doppelpfeile swap.






2 Anwendungen
Nachdem nun geklärt ist, was Heaps eigentlich sind und wie sie funktionieren, möchte ich, bevor wir zur Implementierung kommen, noch kurz zwei kleine Anwendungen von Heaps besprechen.
2.1 Priority Queues
Zum Einen werden Heaps verwendet, um Priority-Queues zu implementieren. Man baut sich einfach einen Heap mit allen in der Queue befindlichen Elementen auf. Wird das nächste Elemente angefordert, führt man einfach deleteMin aus und gibt das kleinste Element zurück. Das Einfügen in die Queue ist ein simples Einfügen in den Heap.
template <typename T> class PriorityQueue { public: T deleteMin() { T item = heap_.getMin(); heap_.deleteMin(); return item; } void insert(T const& item) { heap_.insert(item); } private: Heap<T> heap_; }Ausgefeiltere Implementierungen lassen vielleicht auch noch die Angabe eines Vergleichsoperators zu.
Möchte man allerdings auch Dinge, wie das Löschen von Elementen oder das Verändern von Prioritäten (also Schlüsseln im Heap) unterstützen, wird die Sache etwas kniffliger und lässt sich auch nicht mehr ganz so effizient implementieren. Die Performance-Garantien im O-Kalkül können aber eingehalten werden. Mit noch etwas Mehraufwand lässt sich sogar die join-Operation, also die Vereinigung zweier Warteschlangen zu einer großen effizient implementieren. Aber dazu wird es vielleicht irgendwann mal einen eigenen Artikel geben.
2.2 Heapsort
Wie kann man nun mit Heaps sortieren? Auch das ist recht naheliegend.
Man fügt alle Elemente, die man sortieren möchte, in den Heap ein und holt sie nacheinander mit deleteMin wieder heraus.Das sind n Insert-Operationen und n delete-Min-Operationen. Beide Einzeloperationen haben jeweils eine Laufzeit von O(log n). Heapsort hat also eine Laufzeit von O(n log n) und gehört damit zu den effizienten Sortierverfahren. Es benötigt immer, auch im worst-case maximal 2n log n Vergleiche.
3 Implementierung
So, nun kommen wir zum spannenden Teil. Wie implementiert man sowas effizient? Den Baum wirklich als Baum mit Parent- und Childpointern abzuspeichern wäre ziemlich ineffizient. Durch den strikten Aufbau des Baumes kann man ihn allerdings sehr einfach in einem Array abspeichern.
Dazu schauen wir uns noch einmal den Baum an und nummerieren die Knoten durch, indem wir sie Zeile für Zeile jeweils von links nach rechts durchlaufen.

Nun legen wir den Baum in einem Array ab, indem wir jeden Knoten an den Index legen, der seiner Nummerierung entspricht.
Das sieht so aus:[ ?, 2, 4, 6, 7, 9, 8, ? ]Die Frage ist:
Warum beginnnen wir nicht, wie jeder gute Programmierer bei 0 zu zählen?
Außerdem liegen die Daten nun scheinbar willkürlich in dem Array. Wo ist unser schöner Baum geblieben?Man kann sich aber leicht klar machen, dass man anhand der Indizes sehr leicht immer noch im Baum navigieren kann.
Der Index des Vaterknotens von Knoten i ist einfach i/2.
Die Indizes der Kinderknoten von Knoten i sind 2*i und 2*i+1.
Da der Heap in der letzten Reihe von links nach rechts aufgefüllt wird, kann man durch Vergleich der errechneten Indizes mit der aktuellen Heap-Größe herausfinden, ob das Kind existiert.Vielleicht ist das auch ein guter Grund, seine Arrays ab 1 zu nummerieren.

Alles was wir brauchen, um im Heap zu navigieren sind also Multiplikationen mit 2, Addition und Division durch 2, sowie einige Vergleiche. Das sind sehr einfache und schnelle Operationen, wir können also auf eine sehr schnelle Implementierung hoffen.
Mit der Platzverschwendung des ersten Elements (Index 0) können wir entweder leben, oder aber vor jedem Array-Zugriff vom errechneten Index noch 1 abziehen. Da wir aber so schnell wie möglich sein wollen, verschwenden wir lieber etwas Platz. Zudem macht es die Implementierung etwas einfacher.Nachdem die Idee zur Implementation nun klar ist, können wir loslegen.
3.1 Der Rahmen
template<typename T, size_t MAX_SIZE> class Heap { public: Heap(); T getMin() const; void insert(T const& element); void deleteMin(); private: size_t getFather(size_t i) const { return i/2; } size_t getLeftChild(size_t i) const { return 2*i; } size_t getRightChild(size_t i) const { return 2*i + 1; } bool isRoot(size_t i) const { return i==1; } bool isLastElement(size_t i) const { return i==size_; } size_t getRoot() const { return 1; } bool compare(T const& lhs, T const& rhs) { return lhs < rhs; } T elements_[MAX_SIZE+1]; size_t size_; };Die father/child-Funktionen kapseln die Adressberechnungen, und machen so das Programm lesbarer.
Das ist zunächst mal alles was wir brauchen. Im Konstruktor initialisieren wir den Heap leer. Dazu müssen wir nur die Größe auf 0 setzen.3.2 Konstruktor
template<typename T, size_t MAX_SIZE> Heap::Heap() : size_(0) { }3.3 getMin
Auch getMin ist einfach:
template<typename T, size_t MAX_SIZE> T Heap::getMin() const { assert(size_ != 0); // je nach Geschmack könnte man auch if(...) throw out_of_range schreiben. return elements_[1]; }3.3 insert
So, nun kommen die härteren Brocken. Zur Erinnerung: Bei insert fügen wir das neue Element in der untersten Zeile des Baums soweit links wie möglich ein und lassen es dann nach oben durchsickern.
template<typename T, size_t MAX_SIZE> void Heap::insert(T const& element) { size_t current = ++size_; size_t father = getFather(current); while(!isRoot(current) && compare(element, elements_[father])) { // Wir sind noch nicht an der Wurzel und unser Element ist "kleiner" als der Vater // also sickern wir nach oben elements_[current] = elements_[father]; current = father; father = getFather(current); } elements_[current] = element; }Eine mögliche Optimierung wäre die Platzierung eines Sentinels mit minimalem Key an Stelle 0 im Index. Dann könnte auf die Abfrage !isRoot verzichtet werden. Allerdings gibt es ein solches Element nicht für jeden Typ T.
3.4 deleteMin
Jetzt fehlt nur noch die deleteMin-Methode. Hier wird eine Implementierung der zweiten Variante vorgestellt. Zur Erinnerung: Wir löschen das kleinste Element und füllen die Lücke, indem wir immer das kleinere Kind nach oben ziehen. Anschließend tauschen wir die Lücke mit dem letzten Element des Heaps und lassen es nach oben sickern.
template<typename T, size_t MAX_SIZE> void Heap::deleteMin() { size_t current = getRoot(); size_t child = getLeftChild(current); if(child <= size_) { do { // wenn child nicht das letzte Element (der Knoten also 2 Kinder hat) // wechsle zum rechten Kind, wenn es kleiner ist child += (!isLastElement(child) && compare(elements_[child+1], elements_[child])); elements_[current] = elements_[child]; current = child; child = getLeftChild(current); } while(child <= size_); } // die Lücke ist nun unten angekommen // tausche mit letztem Blatt und vermindere Größe um 1. T element = elements_[size_--]; // jetzt noch das Blatt wieder hochsickern lassen. size_t father = getFather(current); while(!isRoot(current) && compare(element, elements_[father])) { elements_[current] = elements_[father]; current = father; father = getFather(current); } elements_[current] = element; }Damit ist auch die letzte Funktion geschafft.
3.5 Details zur Implementierung
Das war's zunächst mal von der Implementierungsseite. Durch die Kapselung der father/child/isRoot etc.-Funktionen könnte man nun auch leicht die Platzverschwendung bei Element 0 loswerden. father(i) = i/2 bleibt, leftchild(i) = (i+1)*2-1 usw. Allerdings muss man auch in den Funktionen einige Vergleiche mit size_ ändern. Ob und wieviel langsamer es danach ist, müsste man mal nachmessen. Dazu habe ich aber gerade keine Lust. Außerdem stört mich der kleine Platzoverhead nicht. Wir hatten ja sogar festgestellt, dass man ihn als Sentinel nutzen könnte, indem man zum Beispiel bei einem Heap<unsigned int> eine 0 reinschreibt. Auch hier wäre eine Messung interessant, ob es die Performance steigert (laut meinen Messungen bringt es was). Ein heißer Kandidat für solche Messungen ist übrigens heap_sort, oder auch die Verwendung in einer Priority-Queue.
4 Heaps in der STL
Auch die STL bietet eine Implementierung der Datenstruktur Heap, und auch heap-sort ist vorhanden. Die Heaps aus der STL sind Max-Heaps, das heißt an der Wurzel steht das größte Element, nicht wie in unserer Implementierung das kleinste. Das ist natürlich nur eine Frage des Sortierkriteriums.
Im Header <algorithm> sind folgende Funktionen:
void make_heap(RandomAccessIterator beg, RandomAccessIterator end);Baut in der Range einen Heap, indem es die Elemente so umsortiert, dass an der Stelle beg das größte Element steht.
void push_heap(RandomAccessIterator beg, RandomAccessIterator end)Erwartet, dass die Range [beg, end-1) bereits ein Heap ist und fügt diesem das Element an der Stelle end hinzu.
void pop_heap(RandomAccessIterator beg, RandomAccessIterator end)Erwartet, dass [big, end) ein Heap ist und nimmt das größte Element aus dem Heap heraus und legt es an der nun frei werdenden Stelle end ab.
sort_heap(RandomAccessIterator beg, RandomAccessIterator end)Erwartet, dass [beg, end) ein Heap ist und wandelt diesen in eine sortierte Folge um. Danach ist die Sequenz kein Heap mehr!
Jede dieser Funktionen gibt es auch noch in einer weiteren Variante mit einem zusätzlichen Parameter, um das Sortierkriterium festzulegen. Das folgende Codestück zeigt, wie diese Funktionen verwendet werden. Dabei ist zu beachten, dass beim STL-Heap das größte Element Wurzel des Baums ist. Dies hat den Vorteil, dass nachdem alle Elemente aus dem Heap entfernt wurden, das Array direkt aufsteigend sortiert ist.
int data[10] = {11,5,14,12,3,4,9, 8, 20}; make_heap(data,data+9); // erstelle heap, der alle Elemente außer der 20 enhält cout << "groesstes Element: " << data[0] << "\n"; push_heap(data,data+10); // füge 20 hinzu cout << "Neues groesstes Element: " << data[0] << "\n"; cout << "Entferne alle Elemente aus dem Heap: "; for(size_t i=10; i>0;--i) { cout << data[0] << " "; pop_heap(data,data+i); } cout << "\nInhalt des Arrays am Ende: "; for(size_t i=0;i<10;++i) { cout << data[i] << " "; }5 Ausblick
In diesem Artikel wurde gezeigt, was ein binary Heap ist und wie man ihn implementiert. Es sind aber auch noch einige Dinge offen: Der hier vorgestellte Heap ist statisch. Wer ihn dynamisch wachsen lassen möchte, könnte als zugrundeliegende Datenstruktur einen std::vector benutzen. Interessant wäre es auch, das Array über einen Pointer zu adressieren und ähnlich wie die STL-Variante den Heap inplace in einem gegebenen Speicherbereich zu erzeugen. Diese Funktionalität könnte man über einen eigenen Konstruktor bereitstellen. Außerdem wäre es nett, wenn man die Vergleichsfunktion mit angeben könnte. Durch die Verwendug der compare-Funktion für alle Elemente-Vergleiche sollte das kein Problem sein.
Interessant für eine flexiblere Priority-Queue ist die Möglichkeit, Elemente auch wieder zu löschen oder ihren Key zu verändern (vor allem verkleinern). Da es keine Möglichkeit gibt, in einem Heap effizient zu suchen, müsste der Index des Knotens, der gelöscht werden soll, bekannt sein. Dann könnte man ihn einfach mit dem letzten Blatt vertauschen, sodass er gelöscht werden kann. Anschließend muss man den reingetauschten Knoten noch nach unten durchsickern lassen. Möglicherweise wäre es dann interessant, doch eine Funktion siftdown(i) zu implementieren, die das übernimmt. Der Code ist im Prinzip vorhanden. Es ist klar, dass diese Operation in O(log n) Zeit läuft. Damit lässt sich auch das Ändern eines Keys über remove/insert implementieren. Die Laufzeit ist ebenfalls O(log n) Zeit.
Es gibt noch weitere Heaps, man könnte zum Beispiel einen 4-ary Heap oder gar Bäume mit noch höherem Grad bauen. Da viele aktuelle Prozessorarchitekturen allerdings sehr wenig Register haben, wird das nicht viel effizienter als ein binary Heap. In Zukunft könnte das aber anders aussehen. Unterschiedliche Heap-Varianten bieten unterschiedliche Laufzeitgarantien. Für spezielle Anwendungen und wenn es auf Performance wirklich ankommt, lohnt sich also ein Blick auf http://de.wikipedia.org/wiki/Heap_%28Datenstruktur%29. Vielleicht wird es auch noch einen zweiten Teil dieses Artikels geben, in dem dann Pairing-Heaps und Fibonacci-Heaps vorgestellt werden.
6 Quellen
- http://de.wikipedia.org/wiki/Heap_%28Datenstruktur%29
- Algorithmen in C++, Robert Sedgewick, Addison-Wesley (1999)
- Vorlesungsfolien "Algorithm Engineering", Prof. Sanders, Uni KA(SS06)
- The C++ Standard Library, Nicolai M. Josuttis, Addison-Wesley (1999)
-
Hi Jester.
Folgendes ist mir während des Korrigierens noch aufgefallen.
In Abschnitt 4, bei push_heap:
Erwartet, dass die Range [beg, end-1) bereits ein Heap ist und fügt diesem das Element an der Stelle end hinzu.
Müsste das nicht end-1 heißen?
Genauso bei pop_heap:
Erwartet, dass [big, end) ein Heap ist und nimmt das größte Element aus dem Heap heraus und legt es an der nun frei werdenden Stelle end ab.
Btw, schöner Artikel.

-
Danke für die schnelle Korrektur! Ich werde sehen, dass ich sie heute abend noch umsetze.

-
Binary Heaps
Heaps sind eine Datenstruktur, die vor allem bei der Implementierung von Priority-Queues verwendet wird. Die hier vorgestellte Datenstruktur hat nichts mit der Speicherverwaltung von C++ zu tun.
In erster Linie möchte ich binary Heaps vorstellen und zeigen, wie man sie in C++ effizient implementiert. Die Implementierung wird dabei nicht unbedingt mit der, wie sie in klassischen Algorithmenbüchern beschrieben ist, übereinstimmen. Ein Blick dorthinein lohnt sich auf jeden Fall trotzdem noch, um zum Einen eine andere Darstellung zu sehen, und vielleicht auch die klassische Implementierung kennen zu lernen.
Nebenbei wird Heap-Sort, ein Sortierverfahren, das stets mit höchstens 2N*logN Element-Vergleichen sortiert, abfallen. Außerdem wird noch kurz auf die Unterstützung in C++ durch die STL eingegangen.1 Heaps - Die Theorie
Zur einfacheren Darstellung treffen wir zunächst eine vereinfachende Annahme, nämlich dass alle Schlüssel ganze Zahlen sind. Letztlich benötigen wir aber nur die Möglichkeit zu vergleichen.
Ein einfacher Heap bietet nach außen nur drei Operationen an:
- getMin, gibt das kleinste Elemente im Heap zurück.
- insert, fügt einen neuen Knoten in den Heap ein.
- deleteMin, löscht den Knoten mit dem kleinsten Schlüssel aus dem Heap.
getMin hat eine Laufzeit von O(1), alle anderen Operationen haben bei der hier vorgestellten Implementierung eine worst-case Laufzeit von O(log n). Insert hat im Schnitt sogar konstante Laufzeit.
Ein binary Heap ist ein Binärbaum, der zusätzlich folgende Eigenschaften erfüllt:
H1) Er ist soweit wie möglich balanciert, nur die letzte Schicht darf nicht voll besetzt sein. Die letzte Schicht muss linksbündig ausgefüllt sein.
H2) Für jeden Knoten gilt: sein Schlüssel ist kleiner als die Schlüssel seiner Kinder.

Eigenschaft H1) wird uns später eine sehr effiziente Implementierung der Baumstruktur erlauben, Eigenschaft H2) garantiert, dass die Operationen wie deleteMin effizient ausgeführt werden können.
Die Reihenfolge der Kinder eines Knotens ist dagegen beliebig und nicht wie bei einem Suchbaum geordnet. Das linke Kind muss nicht das kleinere sein.Kommen wir nun zu den 3 Operationen.
1.1 getMin
Das ist einfach. Aufgrund der Eigenschaft H2) muss die Wurzel der Knoten mit dem kleinsten Schlüssel sein. Wir können also einfach die Wurzel zurückgeben. Das geht in konstanter Zeit.
1.2 insert
Die insert-Operation ist schon schwieriger. Wir gehen davon aus, dass wir zu Beginn einen korrekten Heap haben.
Beim Einfügen wird der neue Knoten einfach dort eingehängt, wo der nächste Knoten hin muss: In der untersten Ebene soweit links, wie möglich. Damit ist Eigenschaft H1) erfüllt. Leider ist Eigenschaft H2) noch nicht erfüllt.Um den Heap zu "reparieren" vertauschen wir den neu eingefügten Knoten so lange mit seinem Vater, bis die Eigenschaft erfüllt ist.
Im Pseudo-Code sieht das so aus:solange Schlüssel kleiner als der des Vaterknotens: Vertausche Knoten mit seinem VaterDieses nach oben Durchsickern des Knotens heißt auch "sift-up".
Die grünen <-> Pfeile symbolisieren in den folgenden Bildern einen Vergleich, rote Pfeile/Doppelpfeile symbolisieren ein move/swap.


Das Auffinden der richtigen Stelle geht in konstanter Zeit (wie, werden wir in der Implementierung sehen). Der gesamte Baum hat die Höhe log N, daher kann auch sift-up höchstens log N Schritte brauchen. Im Schnitt sind sogar nur O(1) sift-up Schritte pro Einfügung nötig.
1.3 deleteMin
Im Prinzip müssen wir an dieser Stelle nur die Wurzel des Baumes löschen. Allerdings müssen wir die Datenstruktur anschließend noch wieder reparieren.
An dieser Operation scheiden sich ein bisschen die Geister. Die meisten Lehrbücher, zum Beispiel Sedgewick, schlagen folgendes Vorgehen vor:
Entferne die Wurzel und setze an deren Stelle den Knoten, der am weitesten unten rechts im Baum steht. Dadurch erhalten wir wieder einen Baum, der zumindest Eigenschaft H1) erfüllt. Nun lassen wir die neue Wurzel nach unten durchsickern, bis auch Eigenschaft H2) erfüllt ist. Solange sein Schlüssel nicht kleiner ist, als der seiner beiden Kinder, vertausche ihn mit dem Kind mit dem kleineren Schlüssel.




Dieses nach unten Durchsickernlassen des Knotens heißt auch sift-down. Das Vertauschen des Wurzelknotens mit dem Knoten am weitesten unten rechts, sowie das Löschen des Wurzelknotens, geht wieder in konstanter Zeit. Der neue Wurzelknoten kann höchstens bis nach ganz unten in den Baum durchsickern. Also hat deleteMin eine Laufzeit von O(log n).
Etwas unschön ist dabei der Vergleich mit beiden Kindern und der beiden Kinder nochmals untereinander. Man kann das zwar mit 2 Vergleichen hinbekommen, indem zunächst das kleinere Kind ermittelt und dann dieses mit dem Knoten, der durchsickern soll vergleicht, aber es gibt auch eine Alternative, die hier mit einem Vergleich auskommt.
1.3 deleteMin - Alternative
Hier soll nun eine andere Implementierung von deleteMin vorgestellt werden, die diesen Makel beseitigt und dadurch etwas schneller sein könnte. Dieses "schneller" ist allerdings mit Vorsicht zu genießen. Auf meinem Rechner ist diese Implementierung für große Datenmengen etwas schneller als die STL-Implementierung.
Die Idee ist, die Wurzel einfach rauszulöschen und das entstehende Loch nach unten durchsickern zu lassen, indem man immer das kleinere Kind nach oben zieht. Das kostet jeweils nur einen Vergleich. Dadurch landet das Loch nach log(n) Schritten in der untersten Ebene. Nun können wir es mit dem Blatt ganz rechts unten im Baum vertauschen und das Loch endlich wegfallen lassen. Nun müssen wir nur noch den getauschten Knoten wieder nach oben durchsickern lassen. Das geht aber im Schnitt sogar in konstanter Zeit.
Im folgenden Bild bedeuten grüne Doppelpfeile einen Vergleich, rote Pfeile move und rote Doppelpfeile swap.






2 Anwendungen
Nachdem nun geklärt ist, was Heaps eigentlich sind und wie sie funktionieren, möchte ich, bevor wir zur Implementierung kommen, noch kurz zwei kleine Anwendungen von Heaps besprechen.
2.1 Priority Queues
Zum Einen werden Heaps verwendet, um Priority-Queues zu implementieren. Man baut sich einfach einen Heap mit allen in der Queue befindlichen Elementen auf. Wird das nächste Elemente angefordert, führt man einfach deleteMin aus und gibt das kleinste Element zurück. Das Einfügen in die Queue ist ein simples Einfügen in den Heap.
template <typename T> class PriorityQueue { public: T deleteMin() { T item = heap_.getMin(); heap_.deleteMin(); return item; } void insert(T const& item) { heap_.insert(item); } private: Heap<T> heap_; }Ausgefeiltere Implementierungen lassen vielleicht auch noch die Angabe eines Vergleichsoperators zu.
Möchte man allerdings auch Dinge, wie das Löschen von Elementen oder das Verändern von Prioritäten (also Schlüsseln im Heap) unterstützen, wird die Sache etwas kniffliger und lässt sich auch nicht mehr ganz so effizient implementieren. Die Performance-Garantien im O-Kalkül können aber eingehalten werden. Mit noch etwas Mehraufwand lässt sich sogar die join-Operation, also die Vereinigung zweier Warteschlangen zu einer großen effizient implementieren. Aber dazu wird es vielleicht irgendwann mal einen eigenen Artikel geben.
2.2 Heapsort
Wie kann man nun mit Heaps sortieren? Auch das ist recht naheliegend.
Man fügt alle Elemente, die man sortieren möchte, in den Heap ein und holt sie nacheinander mit deleteMin wieder heraus.Das sind n Insert-Operationen und n delete-Min-Operationen. Beide Einzeloperationen haben jeweils eine Laufzeit von O(log n). Heapsort hat also eine Laufzeit von O(n log n) und gehört damit zu den effizienten Sortierverfahren. Es benötigt immer, auch im worst-case maximal 2n log n Vergleiche.
3 Implementierung
So, nun kommen wir zum spannenden Teil. Wie implementiert man sowas effizient? Den Baum wirklich als Baum mit Parent- und Childpointern abzuspeichern wäre ziemlich ineffizient. Durch den strikten Aufbau des Baumes kann man ihn allerdings sehr einfach in einem Array abspeichern.
Dazu schauen wir uns noch einmal den Baum an und nummerieren die Knoten durch, indem wir sie Zeile für Zeile jeweils von links nach rechts durchlaufen.

Nun legen wir den Baum in einem Array ab, indem wir jeden Knoten an den Index legen, der seiner Nummerierung entspricht.
Das sieht so aus:[ ?, 2, 4, 6, 7, 9, 8, ? ]Die Frage ist:
Warum beginnnen wir nicht, wie jeder gute Programmierer bei 0 zu zählen?
Außerdem liegen die Daten nun scheinbar willkürlich in dem Array. Wo ist unser schöner Baum geblieben?Man kann sich aber leicht klar machen, dass man anhand der Indizes sehr leicht immer noch im Baum navigieren kann.
Der Index des Vaterknotens von Knoten i ist einfach i/2.
Die Indizes der Kinderknoten von Knoten i sind 2*i und 2*i+1.
Da der Heap in der letzten Reihe von links nach rechts aufgefüllt wird, kann man durch Vergleich der errechneten Indizes mit der aktuellen Heap-Größe herausfinden, ob das Kind existiert.Vielleicht ist das auch ein guter Grund, seine Arrays ab 1 zu nummerieren.

Alles was wir brauchen, um im Heap zu navigieren sind also Multiplikationen mit 2, Addition und Division durch 2, sowie einige Vergleiche. Das sind sehr einfache und schnelle Operationen, wir können also auf eine sehr schnelle Implementierung hoffen.
Mit der Platzverschwendung des ersten Elements (Index 0) können wir entweder leben, oder aber vor jedem Array-Zugriff vom errechneten Index noch 1 abziehen. Da wir aber so schnell wie möglich sein wollen, verschwenden wir lieber etwas Platz. Zudem macht es die Implementierung etwas einfacher.Nachdem die Idee zur Implementation nun klar ist, können wir loslegen.
3.1 Der Rahmen
template<typename T, size_t MAX_SIZE> class Heap { public: Heap(); T getMin() const; void insert(T const& element); void deleteMin(); private: size_t getFather(size_t i) const { return i/2; } size_t getLeftChild(size_t i) const { return 2*i; } size_t getRightChild(size_t i) const { return 2*i + 1; } bool isRoot(size_t i) const { return i==1; } bool isLastElement(size_t i) const { return i==size_; } size_t getRoot() const { return 1; } bool compare(T const& lhs, T const& rhs) { return lhs < rhs; } T elements_[MAX_SIZE+1]; size_t size_; };Die father/child-Funktionen kapseln die Adressberechnungen, und machen so das Programm lesbarer.
Das ist zunächst mal alles was wir brauchen. Im Konstruktor initialisieren wir den Heap leer. Dazu müssen wir nur die Größe auf 0 setzen.3.2 Konstruktor
template<typename T, size_t MAX_SIZE> Heap::Heap() : size_(0) { }3.3 getMin
Auch getMin ist einfach:
template<typename T, size_t MAX_SIZE> T Heap::getMin() const { assert(size_ != 0); // je nach Geschmack könnte man auch if(...) throw out_of_range schreiben. return elements_[1]; }3.3 insert
So, nun kommen die härteren Brocken. Zur Erinnerung: Bei insert fügen wir das neue Element in der untersten Zeile des Baums soweit links wie möglich ein und lassen es dann nach oben durchsickern.
template<typename T, size_t MAX_SIZE> void Heap::insert(T const& element) { size_t current = ++size_; size_t father = getFather(current); while(!isRoot(current) && compare(element, elements_[father])) { // Wir sind noch nicht an der Wurzel und unser Element ist "kleiner" als der Vater // also sickern wir nach oben elements_[current] = elements_[father]; current = father; father = getFather(current); } elements_[current] = element; }Eine mögliche Optimierung wäre die Platzierung eines Sentinels mit minimalem Key an Stelle 0 im Index. Dann könnte auf die Abfrage !isRoot verzichtet werden. Allerdings gibt es ein solches Element nicht für jeden Typ T.
3.4 deleteMin
Jetzt fehlt nur noch die deleteMin-Methode. Hier wird eine Implementierung der zweiten Variante vorgestellt. Zur Erinnerung: Wir löschen das kleinste Element und füllen die Lücke, indem wir immer das kleinere Kind nach oben ziehen. Anschließend tauschen wir die Lücke mit dem letzten Element des Heaps und lassen es nach oben sickern.
template<typename T, size_t MAX_SIZE> void Heap::deleteMin() { size_t current = getRoot(); size_t child = getLeftChild(current); if(child <= size_) { do { // wenn child nicht das letzte Element (der Knoten also 2 Kinder hat) // wechsle zum rechten Kind, wenn es kleiner ist child += (!isLastElement(child) && compare(elements_[child+1], elements_[child])); elements_[current] = elements_[child]; current = child; child = getLeftChild(current); } while(child <= size_); } // die Lücke ist nun unten angekommen // tausche mit letztem Blatt und vermindere Größe um 1. T element = elements_[size_--]; // jetzt noch das Blatt wieder hochsickern lassen. size_t father = getFather(current); while(!isRoot(current) && compare(element, elements_[father])) { elements_[current] = elements_[father]; current = father; father = getFather(current); } elements_[current] = element; }Damit ist auch die letzte Funktion geschafft.
3.5 Details zur Implementierung
Das war's zunächst mal von der Implementierungsseite. Durch die Kapselung der father/child/isRoot etc.-Funktionen könnte man nun auch leicht die Platzverschwendung bei Element 0 loswerden. father(i) = i/2 bleibt, leftchild(i) = (i+1)*2-1 usw. Allerdings muss man auch in den Funktionen einige Vergleiche mit size_ ändern. Ob und wieviel langsamer es danach ist, müsste man mal nachmessen. Dazu habe ich aber gerade keine Lust. Außerdem stört mich der kleine Platzoverhead nicht. Wir hatten ja sogar festgestellt, dass man ihn als Sentinel nutzen könnte, indem man zum Beispiel bei einem Heap<unsigned int> eine 0 reinschreibt. Auch hier wäre eine Messung interessant, ob es die Performance steigert (laut meinen Messungen bringt es was). Ein heißer Kandidat für solche Messungen ist übrigens heap_sort, oder auch die Verwendung in einer Priority-Queue.
4 Heaps in der STL
Auch die STL bietet eine Implementierung der Datenstruktur Heap, und auch heap-sort ist vorhanden. Die Heaps aus der STL sind Max-Heaps, das heißt an der Wurzel steht das größte Element, nicht wie in unserer Implementierung das kleinste. Das ist natürlich nur eine Frage des Sortierkriteriums.
Im Header <algorithm> sind folgende Funktionen:
void make_heap(RandomAccessIterator beg, RandomAccessIterator end);Baut in der Range einen Heap, indem es die Elemente so umsortiert, dass an der Stelle beg das größte Element steht.
void push_heap(RandomAccessIterator beg, RandomAccessIterator end)Erwartet, dass die Range [beg, end-1) bereits ein Heap ist und fügt diesem das Element an der Stelle end-1 hinzu.
void pop_heap(RandomAccessIterator beg, RandomAccessIterator end)Erwartet, dass [big, end) ein Heap ist und nimmt das größte Element aus dem Heap heraus und legt es an der nun frei werdenden Stelle end-1 ab.
sort_heap(RandomAccessIterator beg, RandomAccessIterator end)Erwartet, dass [beg, end) ein Heap ist und wandelt diesen in eine sortierte Folge um. Danach ist die Sequenz kein Heap mehr!
Jede dieser Funktionen gibt es auch noch in einer weiteren Variante mit einem zusätzlichen Parameter, um das Sortierkriterium festzulegen. Das folgende Codestück zeigt, wie diese Funktionen verwendet werden. Dabei ist zu beachten, dass beim STL-Heap das größte Element Wurzel des Baums ist. Dies hat den Vorteil, dass nachdem alle Elemente aus dem Heap entfernt wurden, das Array direkt aufsteigend sortiert ist.
int data[10] = {11,5,14,12,3,4,9, 8, 20}; make_heap(data,data+9); // erstelle heap, der alle Elemente außer der 20 enhält cout << "groesstes Element: " << data[0] << "\n"; push_heap(data,data+10); // füge 20 hinzu cout << "Neues groesstes Element: " << data[0] << "\n"; cout << "Entferne alle Elemente aus dem Heap: "; for(size_t i=10; i>0;--i) { cout << data[0] << " "; pop_heap(data,data+i); } cout << "\nInhalt des Arrays am Ende: "; for(size_t i=0;i<10;++i) { cout << data[i] << " "; }5 Ausblick
In diesem Artikel wurde gezeigt, was ein binary Heap ist und wie man ihn implementiert. Es sind aber auch noch einige Dinge offen: Der hier vorgestellte Heap ist statisch. Wer ihn dynamisch wachsen lassen möchte, könnte als zugrundeliegende Datenstruktur einen std::vector benutzen. Interessant wäre es auch, das Array über einen Pointer zu adressieren und ähnlich wie die STL-Variante den Heap inplace in einem gegebenen Speicherbereich zu erzeugen. Diese Funktionalität könnte man über einen eigenen Konstruktor bereitstellen. Außerdem wäre es nett, wenn man die Vergleichsfunktion mit angeben könnte. Durch die Verwendug der compare-Funktion für alle Elemente-Vergleiche sollte das kein Problem sein.
Interessant für eine flexiblere Priority-Queue ist die Möglichkeit, Elemente auch wieder zu löschen oder ihren Key zu verändern (vor allem verkleinern). Da es keine Möglichkeit gibt, in einem Heap effizient zu suchen, müsste der Index des Knotens, der gelöscht werden soll, bekannt sein. Dann könnte man ihn einfach mit dem letzten Blatt vertauschen, sodass er gelöscht werden kann. Anschließend muss man den reingetauschten Knoten noch nach unten durchsickern lassen. Möglicherweise wäre es dann interessant, doch eine Funktion siftdown(i) zu implementieren, die das übernimmt. Der Code ist im Prinzip vorhanden. Es ist klar, dass diese Operation in O(log n) Zeit läuft. Damit lässt sich auch das Ändern eines Keys über remove/insert implementieren. Die Laufzeit ist ebenfalls O(log n) Zeit.
Es gibt noch weitere Heaps, man könnte zum Beispiel einen 4-ary Heap oder gar Bäume mit noch höherem Grad bauen. Da viele aktuelle Prozessorarchitekturen allerdings sehr wenig Register haben, wird das nicht viel effizienter als ein binary Heap. In Zukunft könnte das aber anders aussehen. Unterschiedliche Heap-Varianten bieten unterschiedliche Laufzeitgarantien. Für spezielle Anwendungen und wenn es auf Performance wirklich ankommt, lohnt sich also ein Blick auf http://de.wikipedia.org/wiki/Heap_%28Datenstruktur%29. Vielleicht wird es auch noch einen zweiten Teil dieses Artikels geben, in dem dann Pairing-Heaps und Fibonacci-Heaps vorgestellt werden.
6 Quellen
- http://de.wikipedia.org/wiki/Heap_%28Datenstruktur%29
- Algorithmen in C++, Robert Sedgewick, Addison-Wesley (1999)
- Vorlesungsfolien "Algorithm Engineering", Prof. Sanders, Uni KA(SS06)
- The C++ Standard Library, Nicolai M. Josuttis, Addison-Wesley (1999)
-
-predator-: Deine Anmerkungenn zu den stl-funktionen sind richtig. Ich habe die entsprechenden korrekturen vorgenommen.
-
Du hast ja gar kein Profil.

Kannst du das bitte noch nachholen?
-
Dieser Thread wurde von Moderator/in GPC aus dem Forum Die Redaktion in das Forum Archiv verschoben.
Im Zweifelsfall bitte auch folgende Hinweise beachten:
C/C++ Forum :: FAQ - Sonstiges :: Wohin mit meiner Frage?Dieses Posting wurde automatisch erzeugt.