[X] Zufälle gibt's?!

SideWinder

Und nutze dein Wissen für die Auslosung, wehe da gehts nicht mit rechten Dingen zu! *insider*

MfG SideWinder

Jochen Kalmbach

Als Literatur-Ergänzung würde ich noch folgendes freie Buch aufnehmen:

Numerical Recipes in C
Speziell das Kapitel 7:
7 Random Numbers
7.0 Introduction 274
7.1 Uniform Deviates 275
7.2 Transformation Method: Exponential and Normal Deviates 287
7.3 Rejection Method: Gamma, Poisson, Binomial Deviates 290
7.4 Generation of Random Bits 296
7.5 Random Sequences Based on Data Encryption 300
7.6 Simple Monte Carlo Integration 304
7.7 Quasi- (that is, Sub-) Random Sequences 309
7.8 Adaptive and Recursive Monte Carlo Methods 316

ADD: Hmmm... die PDF-Dateien waren auch mal wirklich "frei"... jetzt braucht man da irgendein Plugin für Acrobat...
Also hier kann man die "original" Dateien runterladen:
http://www.fizyka.umk.pl/nrbook/
http://www.ma.utexas.edu/documentation/nr/bookcpdf/
http://202.38.126.65/mathdoc/Numerical Recipes in C/

Marc++us schrieb:

Damit's völlig klar wird, was ich meine. Was würde Dir denn besser gefallen?

Nee, für die Klarheit ist das perfekt. Passt schon

Jester

Marc++us schrieb:

Damit's völlig klar wird, was ich meine. Was würde Dir denn besser gefallen?

if((count - 1) & count == 0) ...

Ist aber leicht verschleiernd.

An eben jenes dachte ich auch. Aber die ausgeschriebene Variante ist (zur Erklärung) definitiv besser.

Marc++us

Zufälle gibt's!

Der folgende Artikel soll gerade für Einsteiger an einem Stück das Thema der Zufallszahlen im Computer beleuchten, und viele immer wieder nachgefragten Irrtümer und Fehlannahmen ausräumen.

Albert Einstein schrieb:

Das, wobei unsere Berechnungen versagen,
nennen wir Zufall.

Die Erzeugung von Zufallszahlen am Computer ist ein beliebtes Beispiel, das einem in jedem Programmierkurs irgendwann begegnet. Aber das obige Zitat von Albert Einstein deutet bereits das Grundproblem an, dem man am Computer bei der Erzeugung von Zufallszahlen begegnen wird: der Computer kann nur rechnen. Ohne zu versagen. Ist dann die Erzeugung von zufälligen Zahlen am Computer nicht bereits ein Widerspruch?

Bevor wir uns mit dieser schon fast philosophischen Frage befassen, beginnen wir mit den Grundlagen der Zufallszahlen in den heute typischen Programmiersprachen.

Der Würfel ist gefallen

In der Bibliothek cstdlib befindet sich die Funktion rand() , die freundlicherweise eine Zufallszahl zwischen 0 und einer Konstante RAND_MAX liefert. Diese Konstante hat üblicherweise den Wert 32767 – offensichtlich lassen sich mit dieser Funktion keine Zufallszahlen erzeugen, die größer sind, also zum Beispiel zwischen 0 und 1000000. Diesem Problem widmen wir uns aber später.

Die andere Frage ist, wie man die zurück gelieferte Zahl auf den gewünschten Wert zuschneidet, ein Würfel oder ein Münzwurf brauchen ja Zufallszahlen in einem Bereich von 1…6 oder 0 und 1, man muss den Wertebereich also anpassen. Die Mathematik bietet dafür die Möglichkeit, den Modulus einer Zahl zu berechnen, das ist der Rest, der bei einer Division durch eine Ganzzahl übrig bleibt. Wikipedia weiß einiges dazu

http://de.wikipedia.org/wiki/Modulo_(Rest)

- aber das schreit nach einem Beispiel:

#include <iostream>
using namespace std;

int main()
{
   for (unsigned u = 0; u < 20; u++)
   {
      cout << u << "\t" << (u % 6) << endl;
   }

   return 0;
}

Dieses kleine Programm zählt von 0 bis 19, in der linken Spalte steht die Zahl, in der rechten Spalte jeweils die Zahl Modulus 6 – in C und C++ wird dies als u % 6 geschrieben. Damit ist es also möglich, das Intervall der gelieferten Zahl wunschgemäß zu beschneiden. Dass die Zahlen immer auf den Bereich 0 bis 5 zugeschnitten werden, sollte nicht weiter stören, eine Addition von 1 wird den Bereich auf 1 bis 6 anheben. Lassen wir nun ein Programm würfeln.

#include <iostream>
#include <cstdlib>
using namespace std;

int main()
{
   for (unsigned u = 0; u < 20; u++)
   {
      cout << 1 + [c]rand()[/c] % 6 << endl;
   }

   return 0;
}

Wunderbar! 20mal wird nun gewürfelt, alle Zahlen liegen zwischen 1 und 6. Gäbe es mit diesem Programm nicht ein paar kleine Probleme, wäre die Sache bereits als gelöst zu betrachten.

Eine allgemeine Formel für Werte aus einem bestimmten Bereich

Zunächst sollte aber dieses Zwischenergebnis festgehalten werden – um eine Zufallszahl zwischen zwei Grenzen a und b zu erhalten, kann man immer die folgende Berechnung verwenden:

zahl = a + [c]rand()[/c] % (b – a + 1);

Für einen Münzwurf – wo nur Zahlen zwischen 0 und 1 benötigt werden – ergibt sich daraus:

zahl = 0 + [c]rand()[/c] % (1 – 0 + 1);

also

zahl = [c]rand()[/c] % 2;

In eine Funktion random gepackt ergibt sich dieses Beispiel (diesmal müssen die Lottozahlen herhalten):

#include <iostream>
#include <cstdlib>

int random(int lowerbounds, int upperbounds)
{
   return lowerbounds + std::[c]rand()[/c] % (upperbounds - lowerbounds + 1);
}

using namespace std;

int main()
{
   for (unsigned u = 0; u < 20; u++)
   {
      cout << random(1, 49) << endl;
   }

   return 0;
}

Da ist nur noch eine kleine Kleinigkeit anzumerken... die Differenz der beiden Grenzen darf natürlich nicht größer RAND_MAX werden. Denn da die Funktion rand() nur Zahlen zwischen 0 und RAND_MAX liefert, kann ein größeres Intervall mit diesem Ansatz nicht abgedeckt werden. Eine Erweiterung der Funktion random() um eine entsprechende Sicherheitsprüfung macht Sinn:

#include <cassert>

int random(int lowerbounds, int upperbounds)
{
   assert(upperbounds - lowerbounds < RAND_MAX);
   return lowerbounds + std::[c]rand()[/c] % (upperbounds - lowerbounds + 1);
}

Sollte diese Bedingung irgendwann einmal verletzt sein, wird das Programm an dieser Stelle eine Assertion anzeigen. Übrigens, es mit dieser Funktion durchaus möglich, Zahlen aus einem größeren Wertebereich zu erzeugen, oder auch negative Zahlen. Gültig ist also:

zahl = random(-10, 10);
   zahl = random(100000, 110000);

Nur die Bedingung des Wertebereichs darf nicht verletzt werden, die Lage der Grenzen selbst innerhalb des Zahlenraums von int spielt keine Rolle.

Eine Formel, die würfelt

Wiederholen Sie das Würfelprogramm mehrfach:

#include <iostream>
#include <cstdlib>
#include <cassert>

int random(int lowerbounds, int upperbounds)
{
   assert(upperbounds - lowerbounds < RAND_MAX);
   return lowerbounds + std::[c]rand()[/c] % (upperbounds - lowerbounds + 1);
}

using namespace std;

int main()
{
   for (unsigned u = 0; u < 20; u++)
   {
      cout << random(1, 6) << endl;
   }

   return 0;
}

Ganz schön einfallslos, unser Gegenspieler – egal wie oft das Programm gestartet wird, immer legt es mit der Zahlenfolge 6, 6, 5, 5, 6, 5, usw., los. Warum ist das so? Gehen wir zu Albert Einstein zurück – der Computer kann eben nicht würfeln, folglich rechnet er. Würden Sie in die Funktion rand() innerhalb der Bibliothek schauen, so fänden Sie dort folgende Zeilen (je nach Compiler kann die genaue Form etwas anders aussehen, das Prinzip bleibt aber immer gleich):

static long holdrand = 1L;
int rand(void)
{
   return (((holdrand = holdrand * 214013L + 2531011L) >> 16) & 0x7fff);
}

Wo ist denn hier der Zufall? Eine simple Formel… ein paar seltsame Zahlen… das war's bereits. Man kann sehen, dass das Ergebnis der Berechnung nicht nur zum Aufrufer zurückgegeben wird, sondern auch in der statischen Variablen holdrand gesichert wird. Offensichtlich realisiert diese Funktion also eine Iteration, jedes Ergebnis hängt immer vom Ergebnis des Vorgängers ab. Aber beim Programmstart beginnt immer alles mit dem gleichen Startwert, denn holdrand wird mit 1 initialisiert (dieser Startwert wird bei einem Zufallszahlengenerator übrigens Seed genannt). Offensichtlich ist das alles ein großer Bluff, denn eine Formel gaukelt nur zufällige Zahlen vor, und wenn man das Programm wiederholt startet, liefert die Formel immer und immer wieder die gleichen Zahlen.

Die hier vorgestellte Formel basiert auf der Methode der linearen Kongruenz, die 1951 von Lehmer vorgestellt wurde, um N Zufallszahlen zu erstellen:

a[0] = seed;
for (i = 1; i <= N; i++)
   a[i] = (a[i – 1] * b + 1) % m;

Die Auswahl der richtigen Zahlen für seed, b und m ist keine triviale Aufgabe, denn die Formel muss gewisse Bedingungen erfüllen, die man an mathematische Zufallszahlen stellt:

Wenn man sehr oft die Formel wiederholt, sollen alle Zahlen mit der ungefähr gleichen Verteilung gezogen werden
Die Zahlen sollen in beliebiger Reihenfolge erscheinen

Für diese Zufallszahlengeneratoren gibt es zahlreiche statistische Tests, die die Bedingungen überprüfen. Glück für uns, dass jemand die Tests für die Funktion rand() in der Standardbibliothek bereits ausgeführt hat, und dass geeignete Werte für b und m gefunden wurden.
Robert Sedgewick gibt in seinem Buch "Algorithmen in C" einen Einblick in die Thematik der Erzeugung von eigenen Zufallszahlenformeln. Auch Donald E. Knuth widmet sich in seinem "The Art Of Computer Programming, Vol. 2" diesem Thema.

Algorithmen in C | ISBN: 3827371821
The art of computer programming | ISBN: 0201896842

Kommen wir wieder zurück zur Praxis: wir wissen nun, warum nach jedem Programmstart immer die gleichen Zahlen erscheinen. Aber gelöst ist das Problem immer noch nicht.

Zeiten und Zufälle

Lustigerweise ist die Lösung für dieses Problem höchstwahrscheinlich wesentlich älter als Sie, lieber Leser, es sind.

Ein Rückblick ins Jahr 1981. Im BASIC-Handbuch des Sinclair ZX81, einem 8-Bit-Rechner mit Folientastatur und 1kB RAM, findet sich folgende Passage:

RAND
RAND <startwert>

Mit RAND können Sie einen neuen Startwert für die Zufallszahlenberechnung mit RND festlegen. Der gleiche Startwert führt immer zur gleichen Folge von Zufallszahlen. So etwas wie "echte" Zufälligkeit erreichen Sie mit "RAND 0". Dabei wird der Startwert aus der Laufzeit des Computers ermittelt.

Um also zufälliger zu werden, brachte man eine Zeit ins Spiel. Die Überlegung ist, dass je nach Laufzeit des Computers der interne Timer einen anderen Wert hat. Den gerade aktuellen Wert des Timers verwendet man nun als Startwert der Zufallsgeneratorfolge – die Wahrscheinlichkeit einer Wiederholung wird nun fast auf 0 gebracht, da selbst nach einem Einschalt- und Bootvorgang nie die gleiche Zeit erreicht wird, ein kleiner Zeitunterschied stellt sich immer ein. Und den Startwert des Zufallszahlengenerators, den Seed, kann man in C++ mit der Funktion srand() setzen.

Erweitern Sie das letzte Würfelprogramm um zwei Zeilen, und staunen Sie:

#include <ctime>  // <-- Neu

...

int main()
{
   srand(static_cast<int>(time(NULL)));  // <-- Neu
   for (unsigned u = 0; u < 20; u++)
   {
      cout << random(1, 6) << endl;
   }

   return 0;
}

Endlich, nach mehrfachem Starten des Programms ergibt sich jedes Mal eine andere Zahlenfolge.

Viel hilft viel – nicht immer

Auf eine böse Falle will ich noch hinweisen, es handelt sich hier um einen beliebten Fehler, den man überraschend oft in Programmen findet. Wohlmeinende Programmierer setzen nämlich vor jeder Ziehung den Startwert aus der Zeit erneut. Werden aber nun Zahlen schneller gezogen als die Uhr tickt, erhalten Sie statt vieler unterschiedlicher Zahlen plötzlich immer den gleichen Wert. Das ist umso dramatischer, da time() ein Sekundentimer ist, und innerhalb einer Sekunde kann man ziemlich oft eine Zufallszahl ziehen.

Probieren Sie es einmal aus.

#include <iostream>
#include <cstdlib>
#include <ctime>
#include <cassert>

int random(int lowerbounds, int upperbounds)
{
   assert(upperbounds - lowerbounds < RAND_MAX);
   return lowerbounds + std::[c]rand()[/c] % (upperbounds - lowerbounds + 1);
}

using namespace std;

int main()
{
   for (unsigned u = 0; u < 20; u++)
   {
      srand(static_cast<int>(time(NULL)));
      cout << random(1, 6) << endl;
   }

   return 0;

Gegen so einen Zufall spielt man gerne! Sehr leicht ist zu sehen, dass immer die gleiche Zahl angezeigt wird – wenn Sie richtig viel Glück haben (man kann dann von Zufall sprechen) erwischen Sie gerade den Sekundenwechsel innerhalb von time() , dann sehen Sie zwei Zahlen. Aber nun ist es wieder vorbei mit dem Zufall. Der wiederholte Aufruf der Funktion srand() setzt die Formel immer wieder auf den gleichen Startwert, da sich die Zeit nicht schnell genug ändert.

Die Klasse für den Zufall

Es ist ja reichlich unhandlich, immer irgendwo das srand() im Programm zu platzieren, damit es nicht vergessen wird. Auch haben Sie ja bereits gelernt, wie man Zufallszahlen in einem Intervall erzeugt. Es wäre an der Zeit, das nun in eine kleine handliche Hilfsklasse zu packen, so dass sie für eigene Programme immer zur Verfügung steht.

// Datei: random.cpp
#ifndef _RANDOM_H
#define _RANDOM_H

#include <cstdlib>
#include <ctime>
#include <cassert>

class Random
{
private:
   Random()
   {
      std::srand(static_cast<int>(std::time(NULL)));
   }
public:
   static int rnd(int lowerbounds, int upperbounds)
   {
      static Random dummy;
      assert(upperbounds - lowerbounds < RAND_MAX);
      return lowerbounds + std::[c]rand()[/c] % (upperbounds - lowerbounds + 1);
   }
};

#endif

Die Klasse wendet einen kleinen Trick an, um den Zufallszahlengenerator zu initialisieren. Die Initialisierung soll nur ein einziges Mal durchgeführt werden, vor dem ersten Aufruf der Memberfunktion rnd() . Dies kann dadurch erreicht werden, dass man innerhalb von rnd() eine statische Variable anlegt, diese wird ganz zu Beginn des Programms initialisiert. Das Dumme ist nur, dass srand() leider keinen return-Wert hat, die an sich nahe liegende Konstruktion dummy = srand(time(NULL)) verbietet sich daher. Als Lösung wird srand() im privaten Konstruktor von Random verkapselt, und innerhalb der Funktion rnd() wird ein statisches Objekt von Random angelegt. Vor der ersten Ausführung von rnd() wird daher garantiert der Konstruktor Random::Random aufgerufen, und damit der Zufallszahlengenerator über die Zeit initialisiert.

Als Demoprogramm spielen wir diesmal Schere, Stein, Papier:

#include <iostream>
#include "random.cpp"

using namespace std;

int main()
{
   char* hand[] = {"Schere", "Stein", "Papier"};

   for (unsigned u = 0; u < 20; u++)
   {
      cout << hand[Random::rnd(0, 2)] << endl;
   }

   return 0;
}

Der Blick über den Tellerrand

Zwei Programmiersprachen, bei denen man Zufallszahlen mit der Zeit initialisieren muss, kennen Sie nun schon: das BASIC des ZX81, und C++. Sie können sich leicht denken, dass auch C sich gleich verhält. Wie sieht es mit anderen Sprachen aus?

In PHP wurde ab der Version 4.2.0 eine interne Erweiterung durchgeführt, seitdem muss vor dem Aufruf von rand() kein srand() mehr ausgeführt werden. Bei älteren Versionen ist auch weiterhin die Zeitinitialisierung notwendig:

<? php
   srand((double)microtime()*1000000); // vor Version 4.2.0
   for($i = 0; $i < 10; $i++)
   {
      $Zufallszahl = rand(0, 100);
      echo ($Zufallszahl."<br/>");
   }
?>

Java stellt eine Klasse Random zur Verfügung, die über zwei Konstruktoren verfügt:

public Random();
public Random(long seed);

Erzeugt man das Objekt der Klasse mit dem parameterlosen Konstruktor, also in dieser Form:

Random rnd = new Random();

so wird das Objekt ebenfalls mit der Systemzeit initialisiert. Als Alternative kann man dem Konstruktor einen eigenen Startwert übergeben.

Auch beim Entwurf von .NET hat Microsoft an dieses Thema gedacht, und erlaubt eine automatische Initialisierung der Klasse System.Random , ohne dass sich der Programmierer darum kümmern muss:

Random rnd = new Random();
int Zufallszahl = rnd.Next(1, 6);

Somit sind die Programmierer der Sprachen C# und VB.NET ebenfalls von der Last befreit, an die Zeitinitialisierung zu denken.

Es gibt übrigens noch andere Möglichkeiten einen Startwert zu setzen, als auf Zeiten zurückzugreifen. Manche Verschlüsselungsprogramme oder Applets für Online-Banking verwenden zufällige Mausbewegungen oder Tastatureingaben, das Programm misst den Verfahrweg der Maus über eine gewisse Zeit, oder die Dauer zwischen den Tastenanschlägen bei der Eingabe, und generiert daraus einen Startwert. Das macht durchaus Sinn, denn gerade solche Programme müssen sich einer Reproduzierbarkeit auf jeden Fall entziehen, würde man hier sich nur auf einen sekundenbasierten Systemtimer verlassen, wäre die Möglichkeit der Manipulation gegeben.

Verteilungsgerechtigkeit

Gemäß der Ausführungen zur Formel, die die Zufallszahlen generiert, sind die Zahlen weitgehend gleichmäßig verteilt. Nehmen wir zunächst also als Voraussetzung an, dass unsere Funktion rand() das Gesetz der großen Zahl tatsächlich erfüllt, und wir bei 1 Billion Ziehungen alle Zahlen gleich oft erhalten.

An dieser Stelle kommt nun ein möglicherweise unangenehmer Effekt zum Tragen, der aus dem Abschneiden der Zufallszahlen kommt. Nehmen Sie das Beispiel Schere, Stein, Papier. Benötigt werden nur Zufallszahlen von 0 bis 2, drei Stück an der Zahl. Erzeugen können wir Zahlen von 0 bis RAND_MAX (32767), das sind genau 32768 unterschiedliche Werte. Und diese Zahl ist nicht durch drei teilbar. Um das Problem zu verstehen, betrachten Sie dieses Programm:

#include <iostream>
using namespace std;

int main()
{
   for (unsigned u = 0; u <= RAND_MAX; u++)
   {
      cout << u << "\t" << u % 3 << endl;
   }
   return 0;
}

Am Anfang geht's noch sauber los:

aber am Ende ist ein kleines Problem vorhanden:

Es geht nicht auf! Der größtmögliche Wert 32767 – der Zufallszahlengenerator schneidet wegen &0xffff alles darüber ab – wird durch das Modulo 3 auf 1 gesetzt. Sie können sich das wie das Ablegen von Kugeln vorstellen, man legt immer reihum in die drei Töpfe, zählt man am Ende die Kugeln in den drei Töpfen 0, 1 und 2, so liegt diese Anzahl von Kugeln pro Topf vor:

Topf 0:   10923   33,33435%
Topf 1:   10923   33,33435%
Topf 2:   10922   33,33130%

Der Unterschied ist noch nicht so dramatisch und wirkt sich erst in der 5ten Stelle aus, aber offensichtlich würde die Schere-Stein-Papier-Software das Papier (da Topf 2 auf Papier abgebildet wird) geringfügig seltener ziehen. Spielt das Programm gegen einen menschlichen Spieler, so wird bei der geringen Anzahl an Ziehungen dieser Effekt gar nicht auffallen. Handelt es sich aber um eine viele millionenmal wiederholte Ziehung für eine Simulation, kann sich diese Bevorzugung irgendwann bemerkbar machen. Man kann diesen Effekt dramatisch vergrößern, wenn die Zufallszahlen nicht aus einem kleinen Intervall stammen müssen, sondern aus einem sehr großen. Nehmen Sie an, Sie benötigen für eine Simulation Zufallszahlen zwischen 0 und 9999. Lassen Sie uns mit einem Programm zählen, wie viele Kugeln in welcher Kiste landen.

#include <iostream>
using namespace std;

int main()
{
   int topf[10000];
   for (int i = 0; i < 10000; i++)
      topf[i] = 0;

   for (unsigned u = 0; u < RAND_MAX; u++)
   {
      topf[u % 10000]++;
   }

   cout << topf[0] << endl;
   cout << topf[9999] << endl;

   return 0;
}

Wir verzichten auf die Ausgabe aller 10000 Töpfe, aber bereits diese Ausgabe sollte Sie schockieren:

4
3

Eine satte Abweichung von 33%. Das ist auch klar: Zahlen ab 30000 werden wieder in die ersten Töpfe abgebildet, aber ab der Zahl 32768 gibt's keine weiteren Zahlen mehr, der Generator erzeugt wieder Zahlen ab 0, die ebenfalls in die ersten Töpfe "geworfen" werden. Daraus ergibt sich ein massives Ungleichgewicht. Wo ist die Grenze? Nun, die lässt sich leicht berechnen (32768 – 3 * 10000 – 1), sie liegt beim Topf 2767, ergänzen Sie noch die Ausgabe um:

cout << topf[2766] << endl;
   cout << topf[2767] << endl;

Folglich erhalten die ersten 2767 Töpfe (als etwa ein Viertel) im Einzelvergleich 33% mehr Treffer als die restlichen Töpfe. Das auf diese Art und Weise erzeugte "zufällige" System hat einen deutlichen Drall. Ob dies in der Anwendung störend ist kann man pauschal nicht sagen, dafür müsste man schon das Anwendungsgebiet kennen. Aber eine Simulation kann hier bereits deutliche und ungewollte Verzerrungen erfahren.

In der folgenden Abbildung sehen Sie die Auswirkung bei den ersten 100 Zahlen.

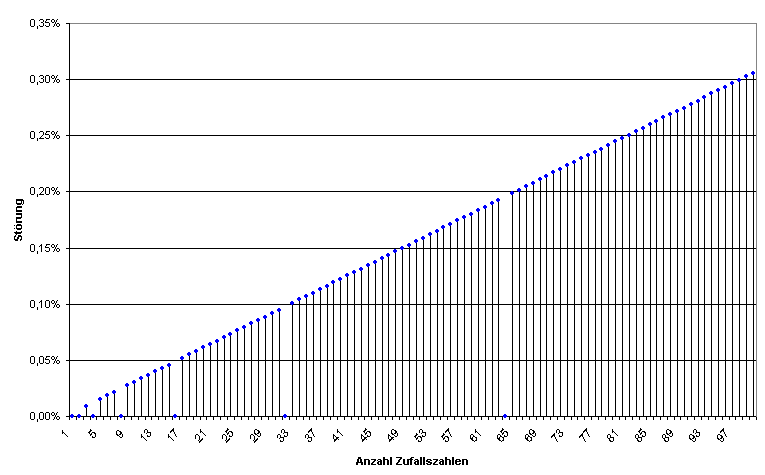
Offensichtlich ist hier, dass die Störung, also die Abweichung der Häufigkeit zwischen der um eins häufiger gezogenen Zahl und den benachteiligten Zahlen, mit zunehmender Größe des Zahlenintervalls zunimmt. Aber auffallend sind die Lücken, die bei den Zahlen 2, 4, 8, 16, 32 und 64 liegen. Dies gilt auch allgemein: bei den Zweierpotenzen gibt es diese Abweichung nicht, da in diesen Fällen 32768 genau ohne Rest durch die Zahl teilbar ist. Und da es keinen Rest, keinen Überlauf, gibt, wird auch kein Topf bevorzugt.

Betrachtet man die gesamte Darstellung für alle möglichen Intervallgrößen, ergibt sich ein relativ dramatisches Bild:

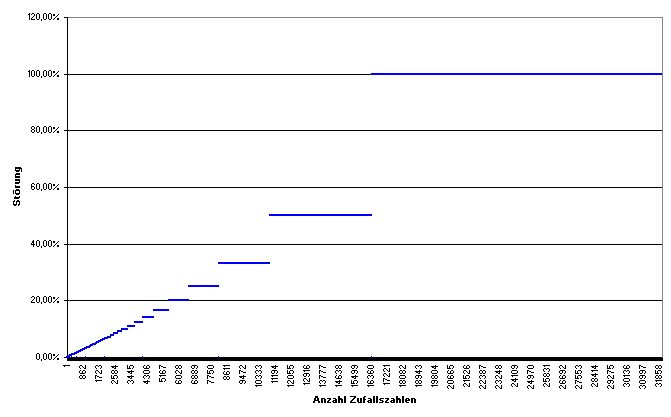
Für sehr große Intervalle wird die Störung extrem, sie liegt bei 100% - im Klartext heißt das, dass die unteren Töpfe im Extremfall doppelt so viele Zahlen erhalten wie die oberen. Aber auch hier sieht man die Lücken bei 4096, 8192 und 16384.

Mehr Gerechtigkeit

Ein erkanntes Problem ist schon fast ein gelöstes Problem. Es gibt drei grundsätzliche Möglichkeiten, mit dieser Ungleichverteilung umzugehen:

Sie ignorieren es, weil es in Ihrer Anwendung vernachlässigbar ist und keine Auswirkung hat
Sie haben kein Problem damit, da die Anzahl der benötigten Zufallszahlen eine Zweierpotenz ist. (Tipp: falls Sie einen Algorithmus entwerfen, der ein größeres Intervall an Zufallszahlen benötigt, macht es daher auch Sinn diesen so zu gestalten, dass die Anzahl benötigter Zufallszahlen einer Zweierpotenz entspricht.)
Sie dürfen die Zahlen aus dem Endbereich des Zufallzahlengenerators nicht berücksichtigen. Dafür folgt sogleich ein Implementationsbeispiel.

Wir erweitern unsere Klasse Random , so dass mit einer zusätzlichen Funktion die Ungleichverteilung nicht mehr stattfinden kann.

static int rnd_nobias(int lowerbounds, int upperbounds)
   {
      static Random dummy;
      assert(upperbounds - lowerbounds < RAND_MAX);

      int rawNumber;
      int count = upperbounds - lowerbounds + 1;

      if (count == 2 || count == 4 || count == 8 || 
          count == 16 || count == 32 || count == 64 || 
          count == 128 || count == 256 || count == 512 || 
          count == 1024 || count == 2048 || count == 4096 || 
          count == 8192 || count == 16384)
          return rnd(lowerbounds, upperbounds);

      /* dieser Programmabschnitt kann auch noch eleganter formuliert
         werden, allerdings ist dann die Wirkung nicht mehr auf den
         ersten Blick erkennbar:
      if ((count - 1) & count == 0)
          return rnd(lowerbounds, upperbounds);
         erfüllt den Zweck ebenfalls
      */

      int ignoreBoundary = (RAND_MAX / count) * count;

      do
      {
         rawNumber = std::[c]rand()[/c];
      } while (rawNumber > ignoreBoundary);

      return lowerbounds + rawNumber % (upperbounds - lowerbounds + 1);
   }

Zunächst prüft die Funktion rnd_nobias() , ob die Mächtigkeit des Wertebereichs eine Zweierpotenz ist, in diesem Fall wird die normale Funktion verwendet. Ansonsten wird eine Grenze berechnet, die angibt ab welchem Schwellwert die unbewerteten Zufallszahlen von rand() verworfen werden. Liegt eine Zahl über diesem Schwellwert, wird die Berechnung wiederholt. Dies geschieht solange, bis die gezogene Zahl unter dem Schwellwert liegt.

Implementationstechnisch ist das übrigens nicht ganz unbedenklich, da hier eigentlich nicht mehr sichergestellt ist, wie lange die Funktion für die Ermittlung der Zahl benötigt, der Funktionsaufruf kann mit einer gewissen (kleinen) Wahrscheinlichkeit sehr lange dauern. Für Echtzeitanwendungen kann dies problematisch sein.

Größere Zufallszahlen

Bisher gilt immer noch die Einschränkung, dass man keine größeren Zufallszahlen als aus einem Intervall der maximalen Mächtigkeit von RAND_MAX ziehen kann. Eine Ziehung einer Zufallszahl zwischen 1 und 1.000.000 ist mit rand() nicht direkt möglich.

Jetzt muss man ein bisschen nachdenken, wie man dieses Ziel doch erreichen kann. rand() liefert maximal 32768 Zufallszahlen, also letztlich 15 zufällige Bits. 1.000.000 benötigt zur binären Darstellung 20 Bits (2^20 = 1.048.576). Was liegt also näher, als hier die Bits von zwei aufeinander folgenden rand() -Ergebnissen miteinander zu kombinieren? Von der ersten Ziehung nimmt man 15 zufällige Bits, und von der zweiten Ziehung die restlichen 5 Bits – und fertig ist eine Zufallszahl im Bereich von 0 bis 1.048.575. Die danach mit Modulo % 1000000 zurecht geschnitten wird.

#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;

int main()
{
   std::srand(static_cast<int>(std::time(NULL)));

   for (unsigned u = 0; u < 20; u++)
   {
      int rnd1 = [c]rand()[/c];
      int rnd2 = [c]rand()[/c];
      int bigrnd = ((rnd1 & 0x1F) << 15) | rnd2;

      cout << bigrnd % 1000000 + 1<< endl;
   }

   return 0;
}

Betrachten Sie die Zusammensetzung der Zahl bigrnd : der Ausdruck rnd1 & 0x1F schneidet die letzten 5 Bit (0x1F entspricht binär 11111) ab (die höheren Bits werden auf 0 gesetzt). Danach wird das Ergebnis um 15 Stellen nach links geschoben, und in den freien Raum rechts wird die Zahl rnd2 komplett – also mit allen 15 Bits – verodert (man könnte statt dem binären Oder auch addieren, das macht in diesem Fall keinen Unterschied, da der Bereich mit Nullen gefüllt ist).

Das ist bereits fast gut. Allerdings müssen Sie an dieser Stelle wieder zur Abbildung 2 zurückgehen und über den Einfluss der Störung nachdenken. Je näher die maximale Zahl an der maximal verfügbaren größten Zahl dran ist, desto größer wird die Störung. Es wäre also besser, wenn man für die Ziehung einer Zufallszahl zwischen 1 und 1.000.000 die Erweiterung nicht nur auf die nächstmögliche Bitgrenze durchführt, sondern darüber hinaus – auf diese Weise reduziert man den Einfluss der ungleichen Häufigkeitsverteilung.

Ein kleiner Hinweis an dieser Stelle: sollte das große Zufallsintervall wieder eine Zweierpotenz sein, so brauchen Sie sich keinen Gedanken über diesen Effekt zu machen, setzen Sie die große Zufallszahl einfach aus den Einzelwerten von rand() zusammen.

Grundsätzlich lässt sich mit diesem hier vorgestellten Kombinationstrick jede Zufallszahl erzeugen, man muss eben ab 30 Bit dreimal rand() aufrufen und kombinieren.

Erweitern Sie nun noch die Klasse Random um eine Zufallszahlerzeugung für rnd32 , also Zufallszahlen im Bereich von 0 bis 4.294.967.296. Das sollte wohl die meisten Wünsche abdecken.

static unsigned int rnd32()
   {
      static Random dummy;
      int rnd1 = [c]rand()[/c];
      int rnd2 = [c]rand()[/c];
      int rnd3 = [c]rand()[/c];
      unsigned int bigrnd = ((rnd1 & 0x03) << 30) + (rnd2 << 15) + rnd3;
   }

Lotto – ganz ohne einstweilige Verfügung

Auch wenn wir zur Zeit online kein Lotto mehr spielen dürfen, soll uns das ja nicht daran hindern, Lottotippgeneratoren zu programmieren. So ein Tippgenerator ist nicht schwer, aber er ist natürlich ein klein wenig kniffliger als ein reines rnd(49) – denn im ersten Schritt zieht man aus 49 Möglichkeiten, dann aus 48, dann aus 47, und so geht das weiter, bis man 6 Zahlen gezogen hat.

Es gibt dafür beliebig viele naive Verfahren – in diesen Fällen sortiert der Programmierer nach jeder Ziehung zum Beispiel ein Array um, oder zieht und prüft, ob er die Zahl bereits gezogen hat. Allen ist gemein, dass sie nicht so effizient sind.

Ein sehr häufig zu findender Ansatz ist die Benutzung der Funktion random_shuffle aus der Klassenbibliothek, die ein vorgegebenes Array durchmischt – und dann nimmt man einfach einen Abschnitt des Arrays. Wie sieht das aus?

#include <iostream>
#include <cstdlib>
#include <ctime>
#include <algorithm>
#include <vector>
#include "random.cpp"
using namespace std;

int main()
{
    srand(static_cast<int>(time(NULL)));
   const unsigned lotto = 49;
   vector<unsigned> numbers(lotto);
   for (unsigned u = 0; u < numbers.size(); u++)
      numbers[u] = u + 1;
   random_shuffle(numbers.begin(), numbers.end());

   for (unsigned u = 0; u < 6; u++)
      cout << numbers[u] << "  ";
   cout << "\n";

   // Sortieren soll auch noch sein? Na gut.
   sort(numbers.begin(), numbers.begin() + 6);
   for (unsigned u = 0; u < 6; u++)
      cout << numbers[u] << "  ";
   cout << "\n";

   return 0;
}

Das ist kurz und knapp, aber für die gesuchte Anwendung nicht optimal, da die Funktion natürlich das gesamte Array durchmischen muss, obwohl eigentlich nur 6 Zahlen gezogen werden sollen.

Übrigens, das Beispiel zeigt Ihnen auch gleich noch, wie man mit Hilfe von sort Teile eines Containers sortieren kann – zwei Iteratoren für Anfang und Ende des Teilarrays sind das notwendige Hilfsmittel.

Vor einiger Zeit wurde dazu im Forum eine sehr schöne Lösung gepostet, so dass es mir natürlich nun schwer fällt glaubhaft zu machen, dass ich das auf meinem ersten Lottotippgenerator vor 20 Jahren auch schon so programmiert hatte. Wie auch immer, hier die genannte elegantere Lösung.

int main()
{
   const unsigned lotto = 49;
   unsigned numbers[lotto];
   for (unsigned u = 0; u < lotto; u++)
      numbers[u] = u + 1;

   unsigned upperbound = lotto;

   for (unsigned u = 0; u < 6; u++)
   {
      upperbound--;
      unsigned index = Random::rnd(0, upperbound);
      cout << numbers[index] << "  ";
      swap(numbers[index], numbers[upperbound]);
   }

   for (unsigned u = 0; u < 6; u++)
      cout << numbers[43 + u] << "  ";
   cout << "\n";

   return 0;
}

Die Idee ist also, das gezogene Element mit dem Element am Ende des Arrays zu vertauschen, und einfach die Obergrenze der gezogenen Zahl immer schrittweise zu vermindern. Am Ende des Algorithmus stehen dann die 6 gezogenen Zahlen sauber aufgereiht in den Feldern numbers[43] bis numbers[48] .

Jetzt muss nur noch das Glück winken...

Zufälle in der Klassenbibliothek

Die Unterstützung für weitere Zufälligkeiten in der C++-Standardbibliothek ist eher gering – außer der zuvor im Lottobeispiel bereits verwendeten Funktion random_shuffle (aus <algorithm> ) zum Mischen eines Containers findet man hier nichts.

Gerade für statistische Anwendungen benötigt man manchmal spezielle Verteilungen, also ein Ziehungsverhalten des Generators, bei dem bestimmte Zahlenbereiche häufiger oder seltener vorkommen. Denn die vorhandene Generatorfunktion von C++ liefert nur eine Gleichverteilung der Zahlen. Will man hier selbst eingreifen, so kann man dies selbst über ein zwischengeschaltetes Array realisieren. Nehmen Sie an, Sie wollen Zahlen von 1 bis 10 ziehen, aber die geraden Zahlen sollen dabei doppelt so oft vorkommen. So etwas lässt sich mit einer Abbildung einfach erreichen:

unsigned distribution[15];
for (unsigned u = 0; u < 10; u++)
{
   distribution[u] = u + 1;
   if ( (u&1) == 0)
      distribution[10 + u / 2] = u + 2;
}

Dies füllt das Array distribution in der Form:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 2, 4, 6, 8, 10

Und der Aufruf von distribution[rnd() % 15] liefert demnach Zufallszahlen von 1 bis 10, bei denen die geraden Zahlen doppelt so oft vorkommen.

Für komplexere Verteilungsabbildungen, insbesondere wenn es um mathematische Verteilungen geht, sollte man aber doch lieber zu einer Bibliothek greifen – glücklicherweise bietet die „Quasi-Standard-Bibliothek“ boost hier unter dem Namen boost::random zahlreiche Lösungen.

Schlusswort

Wer hätte auf den ersten Blick bedacht, dass selbst eine so kleine und schlichte Funktion wie rand() bereits so viele verborgene Geheimnisse besitzt? Wenn also nun wieder jemand im Forum einmal nach dem besten Weg zur Erzeugung von großen Zufallszahlen fragt, oder mit dem Timer sich selbst Steine in den Weg legt – dann hoffe ich doch, dass Sie diesen Artikel verlinken werden.

Literaturempfehlung

Das Ebook "Numerical Recipes in C", erhältlich unter
http://www.fizyka.umk.pl/nrbook/
http://www.ma.utexas.edu/documentation/nr/bookcpdf/
http://202.38.126.65/mathdoc/Numerical Recipes in C/

Speziell das Kapitel 7:
7 Random Numbers
7.0 Introduction 274
7.1 Uniform Deviates 275
7.2 Transformation Method: Exponential and Normal Deviates 287
7.3 Rejection Method: Gamma, Poisson, Binomial Deviates 290
7.4 Generation of Random Bits 296
7.5 Random Sequences Based on Data Encryption 300
7.6 Simple Monte Carlo Integration 304
7.7 Quasi- (that is, Sub-) Random Sequences 309
7.8 Adaptive and Recursive Monte Carlo Methods 316

michba

Zufälle gibt's!

Der folgende Artikel soll gerade für Einsteiger an einem Stück das Thema der Zufallszahlen im Computer beleuchten, und viele immer wieder nachgefragten Irrtümer und Fehlannahmen ausräumen.

Albert Einstein schrieb:

Das, wobei unsere Berechnungen versagen,
nennen wir Zufall.

Die Erzeugung von Zufallszahlen am Computer ist ein beliebtes Beispiel, das einem in jedem Programmierkurs irgendwann begegnet. Aber das obige Zitat von Albert Einstein deutet bereits das Grundproblem an, dem man am Computer bei der Erzeugung von Zufallszahlen begegnen wird: der Computer kann nur rechnen. Ohne zu versagen. Ist dann die Erzeugung von zufälligen Zahlen am Computer nicht bereits ein Widerspruch?

Bevor wir uns mit dieser schon fast philosophischen Frage befassen, beginnen wir mit den Grundlagen der Zufallszahlen in den heute typischen Programmiersprachen.

Der Würfel ist gefallen

In der Bibliothek cstdlib befindet sich die Funktion rand() , die freundlicherweise eine Zufallszahl zwischen 0 und einer Konstante RAND_MAX liefert. Diese Konstante hat üblicherweise den Wert 32767 – offensichtlich lassen sich mit dieser Funktion keine Zufallszahlen erzeugen, die größer sind, also zum Beispiel zwischen 0 und 1000000. Diesem Problem widmen wir uns aber später.

Die andere Frage ist, wie man die zurückgelieferte Zahl auf den gewünschten Wert zuschneidet; ein Würfel oder ein Münzwurf brauchen ja Zufallszahlen in einem Bereich von 1…6 oder 0 und 1, man muss den Wertebereich also anpassen. Die Mathematik bietet dafür die Möglichkeit, den Modulus einer Zahl zu berechnen, das ist der Rest, der bei einer Division durch eine Ganzzahl übrig bleibt. Wikipedia weiß einiges dazu

http://de.wikipedia.org/wiki/Modulo_(Rest)

- aber das schreit nach einem Beispiel:

#include <iostream>
using namespace std;

int main()
{
   for (unsigned u = 0; u < 20; u++)
   {
      cout << u << "\t" << (u % 6) << endl;
   }

   return 0;
}

Dieses kleine Programm zählt von 0 bis 19, in der linken Spalte steht die Zahl, in der rechten Spalte jeweils die Zahl Modulus 6 – in C und C++ wird dies als u % 6 geschrieben. Damit ist es also möglich, das Intervall der gelieferten Zahl wunschgemäß zu beschneiden. Dass die Zahlen immer auf den Bereich 0 bis 5 zugeschnitten werden, sollte nicht weiter stören, eine Addition von 1 wird den Bereich auf 1 bis 6 anheben. Lassen wir nun ein Programm würfeln.

#include <iostream>
#include <cstdlib>
using namespace std;

int main()
{
   for (unsigned u = 0; u < 20; u++)
   {
      cout << 1 + [c]rand()[/c] % 6 << endl;
   }

   return 0;
}

Wunderbar! 20mal wird nun gewürfelt, alle Zahlen liegen zwischen 1 und 6. Gäbe es mit diesem Programm nicht ein paar kleine Probleme, wäre die Sache bereits als gelöst zu betrachten.

Eine allgemeine Formel für Werte aus einem bestimmten Bereich

Zunächst sollte aber dieses Zwischenergebnis festgehalten werden – um eine Zufallszahl zwischen zwei Grenzen a und b zu erhalten, kann man immer die folgende Berechnung verwenden:

zahl = a + [c]rand()[/c] % (b – a + 1);

Für einen Münzwurf – wo nur Zahlen zwischen 0 und 1 benötigt werden – ergibt sich daraus:

zahl = 0 + [c]rand()[/c] % (1 – 0 + 1);

also

zahl = [c]rand()[/c] % 2;

In eine Funktion random gepackt***,*** ergibt sich dieses Beispiel (diesmal müssen die Lottozahlen herhalten):

#include <iostream>
#include <cstdlib>

int random(int lowerbounds, int upperbounds)
{
   return lowerbounds + std::[c]rand()[/c] % (upperbounds - lowerbounds + 1);
}

using namespace std;

int main()
{
   for (unsigned u = 0; u < 20; u++)
   {
      cout << random(1, 49) << endl;
   }

   return 0;
}

Da ist nur noch eine kleine Kleinigkeit anzumerken... die Differenz der beiden Grenzen darf natürlich nicht größer RAND_MAX werden. Denn da die Funktion rand() nur Zahlen zwischen 0 und RAND_MAX liefert, kann ein größeres Intervall mit diesem Ansatz nicht abgedeckt werden. Eine Erweiterung der Funktion random() um eine entsprechende Sicherheitsprüfung ist sinnvoll:

#include <cassert>

int random(int lowerbounds, int upperbounds)
{
   assert(upperbounds - lowerbounds < RAND_MAX);
   return lowerbounds + std::[c]rand()[/c] % (upperbounds - lowerbounds + 1);
}

Sollte diese Bedingung irgendwann einmal verletzt sein, wird das Programm an dieser Stelle eine Assertion anzeigen. Übrigens, es ist mit dieser Funktion durchaus möglich, Zahlen aus einem größeren Wertebereich zu erzeugen, oder auch negative Zahlen. Gültig ist also:

zahl = random(-10, 10);
   zahl = random(100000, 110000);

Nur die Bedingung des Wertebereichs darf nicht verletzt werden, die Lage der Grenzen selbst innerhalb des Zahlenraums von int spielt keine Rolle.

Eine Formel, die würfelt

Wiederholen Sie das Würfelprogramm mehrfach:

#include <iostream>
#include <cstdlib>
#include <cassert>

int random(int lowerbounds, int upperbounds)
{
   assert(upperbounds - lowerbounds < RAND_MAX);
   return lowerbounds + std::[c]rand()[/c] % (upperbounds - lowerbounds + 1);
}

using namespace std;

int main()
{
   for (unsigned u = 0; u < 20; u++)
   {
      cout << random(1, 6) << endl;
   }

   return 0;
}

Ganz schön einfallslos, unser Gegenspieler – egal wie oft das Programm gestartet wird, immer legt es mit der Zahlenfolge 6, 6, 5, 5, 6, 5, usw., los. Warum ist das so? Gehen wir zu Albert Einstein zurück – der Computer kann eben nicht würfeln, folglich rechnet er. Würden Sie in die Funktion rand() innerhalb der Bibliothek schauen, so fänden Sie dort folgende Zeilen (je nach Compiler kann die genaue Form etwas anders aussehen, das Prinzip bleibt aber immer gleich):

static long holdrand = 1L;
int rand(void)
{
   return (((holdrand = holdrand * 214013L + 2531011L) >> 16) & 0x7fff);
}

Wo ist denn hier der Zufall? Eine simple Formel… ein paar seltsame Zahlen… das war's bereits. Man kann sehen, dass das Ergebnis der Berechnung nicht nur zum Aufrufer zurückgegeben wird, sondern auch in der statischen Variablen holdrand gesichert wird. Offensichtlich realisiert diese Funktion also eine Iteration, jedes Ergebnis hängt immer vom Ergebnis des Vorgängers ab. Aber beim Programmstart beginnt immer alles mit dem gleichen Startwert, denn holdrand wird mit 1 initialisiert (dieser Startwert wird bei einem Zufallszahlengenerator übrigens Seed genannt). Offensichtlich ist das alles ein großer Bluff, denn eine Formel gaukelt nur zufällige Zahlen vor, und wenn man das Programm wiederholt startet, liefert die Formel immer und immer wieder die gleichen Zahlen.

Die hier vorgestellte Formel basiert auf der Methode der linearen Kongruenz, die 1951 von Lehmer vorgestellt wurde, um N Zufallszahlen zu erstellen:

a[0] = seed;
for (i = 1; i <= N; i++)
   a[i] = (a[i – 1] * b + 1) % m;

Die Auswahl der richtigen Zahlen für seed, b und m ist keine triviale Aufgabe, denn die Formel muss gewisse Bedingungen erfüllen, die man an mathematische Zufallszahlen stellt:

Wenn man sehr oft die Formel wiederholt, sollen alle Zahlen mit der ungefähr gleichen Verteilung gezogen werden
Die Zahlen sollen in beliebiger Reihenfolge erscheinen

Für diese Zufallszahlengeneratoren gibt es zahlreiche statistische Tests, die die Bedingungen überprüfen. Glück für uns, dass jemand die Tests für die Funktion rand() in der Standardbibliothek bereits ausgeführt hat, und dass geeignete Werte für b und m gefunden wurden.
Robert Sedgewick gibt in seinem Buch "Algorithmen in C" einen Einblick in die Thematik der Erzeugung von eigenen Zufallszahlenformeln. Auch Donald E. Knuth widmet sich in seinem "The Art Of Computer Programming, Vol. 2" diesem Thema.

Algorithmen in C | ISBN: 3827371821
The art of computer programming | ISBN: 0201896842

Kommen wir wieder zurück zur Praxis: wir wissen nun, warum nach jedem Programmstart immer die gleichen Zahlen erscheinen. Aber gelöst ist das Problem immer noch nicht.

Zeiten und Zufälle

Lustigerweise ist die Lösung für dieses Problem höchstwahrscheinlich wesentlich älter als Sie, lieber Leser, es sind.

Ein Rückblick ins Jahr 1981. Im BASIC-Handbuch des Sinclair ZX81, einem 8-Bit-Rechner mit Folientastatur und 1kB RAM, findet sich folgende Passage:

RAND
RAND <startwert>

Mit RAND können Sie einen neuen Startwert für die Zufallszahlenberechnung mit RND festlegen. Der gleiche Startwert führt immer zur gleichen Folge von Zufallszahlen. So etwas wie "echte" Zufälligkeit erreichen Sie mit "RAND 0". Dabei wird der Startwert aus der Laufzeit des Computers ermittelt.

Um also zufälliger zu werden, brachte man eine Zeit ins Spiel. Die Überlegung ist, dass je nach Laufzeit des Computers der interne Timer einen anderen Wert hat. Den gerade aktuellen Wert des Timers verwendet man nun als Startwert der Zufallsgeneratorfolge – die Wahrscheinlichkeit einer Wiederholung wird nun fast auf 0 gebracht, da selbst nach einem Einschalt- und Bootvorgang nie die gleiche Zeit erreicht wird, ein kleiner Zeitunterschied stellt sich immer ein. Und den Startwert des Zufallszahlengenerators, den Seed, kann man in C++ mit der Funktion srand() setzen.

Erweitern Sie das letzte Würfelprogramm um zwei Zeilen, und staunen Sie:

#include <ctime>  // <-- Neu

...

int main()
{
   srand(static_cast<int>(time(NULL)));  // <-- Neu
   for (unsigned u = 0; u < 20; u++)
   {
      cout << random(1, 6) << endl;
   }

   return 0;
}

Endlich, nach mehrfachem Starten des Programms ergibt sich jedes Mal eine andere Zahlenfolge.

Viel hilft viel – nicht immer

Auf eine böse Falle will ich noch hinweisen, es handelt sich hier um einen beliebten Fehler, den man überraschend oft in Programmen findet. Wohlmeinende Programmierer setzen nämlich vor jeder Ziehung den Startwert aus der Zeit erneut. Werden aber nun Zahlen schneller gezogen als die Uhr tickt, erhalten Sie statt vieler unterschiedlicher Zahlen plötzlich immer den gleichen Wert. Das ist umso dramatischer, da time() ein Sekundentimer ist, und innerhalb einer Sekunde kann man ziemlich oft eine Zufallszahl ziehen.

Probieren Sie es einmal aus.

#include <iostream>
#include <cstdlib>
#include <ctime>
#include <cassert>

int random(int lowerbounds, int upperbounds)
{
   assert(upperbounds - lowerbounds < RAND_MAX);
   return lowerbounds + std::[c]rand()[/c] % (upperbounds - lowerbounds + 1);
}

using namespace std;

int main()
{
   for (unsigned u = 0; u < 20; u++)
   {
      srand(static_cast<int>(time(NULL)));
      cout << random(1, 6) << endl;
   }

   return 0;

Gegen so einen Zufall spielt man gerne! Sehr leicht ist zu sehen, dass immer die gleiche Zahl angezeigt wird – wenn Sie richtig viel Glück haben (man kann dann von Zufall sprechen) erwischen Sie gerade den Sekundenwechsel innerhalb von time() , dann sehen Sie zwei Zahlen. Aber nun ist es wieder vorbei mit dem Zufall. Der wiederholte Aufruf der Funktion srand() setzt die Formel immer wieder auf den gleichen Startwert, da sich die Zeit nicht schnell genug ändert.

Die Klasse für den Zufall

Es ist ja reichlich unhandlich, immer irgendwo das srand() im Programm zu platzieren, damit es nicht vergessen wird. Auch haben Sie ja bereits gelernt, wie man Zufallszahlen in einem Intervall erzeugt. Es wäre an der Zeit, das nun in eine kleine handliche Hilfsklasse zu packen, so dass sie für eigene Programme immer zur Verfügung steht.

// Datei: random.cpp
#ifndef _RANDOM_H
#define _RANDOM_H

#include <cstdlib>
#include <ctime>
#include <cassert>

class Random
{
private:
   Random()
   {
      std::srand(static_cast<int>(std::time(NULL)));
   }
public:
   static int rnd(int lowerbounds, int upperbounds)
   {
      static Random dummy;
      assert(upperbounds - lowerbounds < RAND_MAX);
      return lowerbounds + std::[c]rand()[/c] % (upperbounds - lowerbounds + 1);
   }
};

#endif

Die Klasse wendet einen kleinen Trick an, um den Zufallszahlengenerator zu initialisieren. Die Initialisierung soll nur ein einziges Mal durchgeführt werden, vor dem ersten Aufruf der Memberfunktion rnd() . Dies kann dadurch erreicht werden, dass man innerhalb von rnd() eine statische Variable anlegt, diese wird ganz zu Beginn des Programms initialisiert. Das Dumme ist nur, dass srand() leider keinen return-Wert hat, die an sich nahe liegende Konstruktion dummy = srand(time(NULL)) verbietet sich daher. Als Lösung wird srand() im privaten Konstruktor von Random verkapselt, und innerhalb der Funktion rnd() wird ein statisches Objekt von Random angelegt. Vor der ersten Ausführung von rnd() wird daher garantiert der Konstruktor Random::Random aufgerufen, und damit der Zufallszahlengenerator über die Zeit initialisiert.

Als Demoprogramm spielen wir diesmal Schere, Stein, Papier:

#include <iostream>
#include "random.cpp"

using namespace std;

int main()
{
   char* hand[] = {"Schere", "Stein", "Papier"};

   for (unsigned u = 0; u < 20; u++)
   {
      cout << hand[Random::rnd(0, 2)] << endl;
   }

   return 0;
}

Der Blick über den Tellerrand

Zwei Programmiersprachen, bei denen man Zufallszahlen mit der Zeit initialisieren muss, kennen Sie nun schon: das BASIC des ZX81, und C++. Sie können sich leicht denken, dass auch C sich gleich verhält. Wie sieht es mit anderen Sprachen aus?

In PHP wurde ab der Version 4.2.0 eine interne Erweiterung durchgeführt, seitdem muss vor dem Aufruf von rand() kein srand() mehr ausgeführt werden. Bei älteren Versionen ist auch weiterhin die Zeitinitialisierung notwendig:

<? php
   srand((double)microtime()*1000000); // vor Version 4.2.0
   for($i = 0; $i < 10; $i++)
   {
      $Zufallszahl = rand(0, 100);
      echo ($Zufallszahl."<br/>");
   }
?>

Java stellt eine Klasse Random zur Verfügung, die über zwei Konstruktoren verfügt:

public Random();
public Random(long seed);

Erzeugt man das Objekt der Klasse mit dem parameterlosen Konstruktor, also in dieser Form:

Random rnd = new Random();

so wird das Objekt ebenfalls mit der Systemzeit initialisiert. Als Alternative kann man dem Konstruktor einen eigenen Startwert übergeben.

Auch beim Entwurf von .NET hat Microsoft an dieses Thema gedacht, und erlaubt eine automatische Initialisierung der Klasse System.Random , ohne dass sich der Programmierer darum kümmern muss:

Random rnd = new Random();
int Zufallszahl = rnd.Next(1, 6);

Somit sind die Programmierer der Sprachen C# und VB.NET ebenfalls von der Last befreit, an die Zeitinitialisierung zu denken.

Es gibt übrigens noch andere Möglichkeiten***,*** einen Startwert zu setzen, als auf Zeiten zurückzugreifen. Manche Verschlüsselungsprogramme oder Applets für Online-Banking verwenden zufällige Mausbewegungen oder Tastatureingaben, das Programm misst den Verfahrweg der Maus über eine gewisse Zeit, oder die Dauer zwischen den Tastenanschlägen bei der Eingabe, und generiert daraus einen Startwert. Das ergibt durchaus Sinn, denn gerade solche Programme müssen sich einer Reproduzierbarkeit auf jeden Fall entziehen, würde man sich hier nur auf einen sekundenbasierten Systemtimer verlassen, wäre die Möglichkeit der Manipulation gegeben.

Verteilungsgerechtigkeit

Gemäß der Ausführungen zur Formel, die die Zufallszahlen generiert, sind die Zahlen weitgehend gleichmäßig verteilt. Nehmen wir zunächst also als Voraussetzung an, dass unsere Funktion rand() das Gesetz der großen Zahl tatsächlich erfüllt, und wir bei 1 Billion Ziehungen alle Zahlen gleich oft erhalten.

An dieser Stelle kommt nun ein möglicherweise unangenehmer Effekt zum Tragen, der aus dem Abschneiden der Zufallszahlen kommt. Nehmen Sie das Beispiel Schere, Stein, Papier. Benötigt werden nur Zufallszahlen von 0 bis 2, drei Stück an der Zahl. Erzeugen können wir Zahlen von 0 bis RAND_MAX (32767), das sind genau 32768 unterschiedliche Werte. Und diese Zahl ist nicht durch drei teilbar. Um das Problem zu verstehen, betrachten Sie dieses Programm:

#include <iostream>
using namespace std;

int main()
{
   for (unsigned u = 0; u <= RAND_MAX; u++)
   {
      cout << u << "\t" << u % 3 << endl;
   }
   return 0;
}

Am Anfang geht's noch sauber los:

aber am Ende ist ein kleines Problem vorhanden:

Es geht nicht auf! Der größtmögliche Wert 32767 – der Zufallszahlengenerator schneidet wegen &0xffff alles darüber ab – wird durch das Modulo 3 auf 1 gesetzt. Sie können sich das wie das Ablegen von Kugeln vorstellen, man legt immer reihum in die drei Töpfe; zählt man am Ende die Kugeln in den drei Töpfen 0, 1 und 2, so liegt diese Anzahl von Kugeln pro Topf vor:

Topf 0:   10923   33,33435%
Topf 1:   10923   33,33435%
Topf 2:   10922   33,33130%

Der Unterschied ist noch nicht so dramatisch und wirkt sich erst in der 5ten Stelle aus, aber offensichtlich würde die Schere-Stein-Papier-Software das Papier (da Topf 2 auf Papier abgebildet wird) geringfügig seltener ziehen. Spielt das Programm gegen einen menschlichen Spieler, so wird bei der geringen Anzahl an Ziehungen dieser Effekt gar nicht auffallen. Handelt es sich aber um eine viele millionenmal wiederholte Ziehung für eine Simulation, kann sich diese Bevorzugung irgendwann bemerkbar machen. Man kann diesen Effekt dramatisch vergrößern, wenn die Zufallszahlen nicht aus einem kleinen Intervall stammen müssen, sondern aus einem sehr großen. Nehmen Sie an, Sie benötigen für eine Simulation Zufallszahlen zwischen 0 und 9999. Lassen Sie uns mit einem Programm zählen, wie viele Kugeln in welcher Kiste landen.

#include <iostream>
using namespace std;

int main()
{
   int topf[10000];
   for (int i = 0; i < 10000; i++)
      topf[i] = 0;

   for (unsigned u = 0; u < RAND_MAX; u++)
   {
      topf[u % 10000]++;
   }

   cout << topf[0] << endl;
   cout << topf[9999] << endl;

   return 0;
}

Wir verzichten auf die Ausgabe aller 10000 Töpfe, aber bereits diese Ausgabe sollte Sie schockieren:

4
3

Eine satte Abweichung von 33%. Das ist auch klar: Zahlen ab 30000 werden wieder in die ersten Töpfe abgebildet, aber ab der Zahl 32768 gibt's keine weiteren Zahlen mehr, der Generator erzeugt wieder Zahlen ab 0, die ebenfalls in die ersten Töpfe "geworfen" werden. Daraus ergibt sich ein massives Ungleichgewicht. Wo ist die Grenze? Nun, die lässt sich leicht berechnen (32768 – 3 * 10000 – 1), sie liegt beim Topf 2767, ergänzen Sie noch die Ausgabe um:

cout << topf[2766] << endl;
   cout << topf[2767] << endl;

Folglich erhalten die ersten 2767 Töpfe (als etwa ein Viertel) im Einzelvergleich 33% mehr Treffer als die restlichen Töpfe. Das auf diese Art und Weise erzeugte "zufällige" System hat einen deutlichen Drall. Ob dies in der Anwendung störend ist kann man pauschal nicht sagen, dafür müsste man schon das Anwendungsgebiet kennen. Aber eine Simulation kann hier bereits deutliche und ungewollte Verzerrungen erfahren.

In der folgenden Abbildung sehen Sie die Auswirkung bei den ersten 100 Zahlen.

Offensichtlich ist hier, dass die Störung, also die Abweichung der Häufigkeit zwischen der um eins häufiger gezogenen Zahl und den benachteiligten Zahlen, mit zunehmender Größe des Zahlenintervalls zunimmt. Aber auffallend sind die Lücken, die bei den Zahlen 2, 4, 8, 16, 32 und 64 liegen. Dies gilt auch allgemein: bei den Zweierpotenzen gibt es diese Abweichung nicht, da in diesen Fällen 32768 genau ohne Rest durch die Zahl teilbar ist. Und da es keinen Rest, keinen Überlauf, gibt, wird auch kein Topf bevorzugt.

Betrachtet man die gesamte Darstellung für alle möglichen Intervallgrößen, ergibt sich ein relativ dramatisches Bild:

Für sehr große Intervalle wird die Störung extrem, sie liegt bei 100% - im Klartext heißt das, dass die unteren Töpfe im Extremfall doppelt so viele Zahlen erhalten wie die oberen. Aber auch hier sieht man die Lücken bei 4096, 8192 und 16384.

Mehr Gerechtigkeit

Ein erkanntes Problem ist schon fast ein gelöstes Problem. Es gibt drei grundsätzliche Möglichkeiten, mit dieser Ungleichverteilung umzugehen:

Sie ignorieren es, weil es in Ihrer Anwendung vernachlässigbar ist und keine Auswirkung hat
Sie haben kein Problem damit, da die Anzahl der benötigten Zufallszahlen eine Zweierpotenz ist. (Tipp: falls Sie einen Algorithmus entwerfen, der ein größeres Intervall an Zufallszahlen benötigt, ist es daher auch sinnvoll, diesen so zu gestalten, dass die Anzahl benötigter Zufallszahlen einer Zweierpotenz entspricht.)
Sie dürfen die Zahlen aus dem Endbereich des Zufall***s***zahlengenerators nicht berücksichtigen. Dafür folgt sogleich ein ***Implementierungs***beispiel.

Wir erweitern unsere Klasse Random , so dass mit einer zusätzlichen Funktion die Ungleichverteilung nicht mehr stattfinden kann.

static int rnd_nobias(int lowerbounds, int upperbounds)
   {
      static Random dummy;
      assert(upperbounds - lowerbounds < RAND_MAX);

      int rawNumber;
      int count = upperbounds - lowerbounds + 1;

      if (count == 2 || count == 4 || count == 8 || 
          count == 16 || count == 32 || count == 64 || 
          count == 128 || count == 256 || count == 512 || 
          count == 1024 || count == 2048 || count == 4096 || 
          count == 8192 || count == 16384)
          return rnd(lowerbounds, upperbounds);

      /* dieser Programmabschnitt kann auch noch eleganter formuliert
         werden, allerdings ist dann die Wirkung nicht mehr auf den
         ersten Blick erkennbar:
      if ((count - 1) & count == 0)
          return rnd(lowerbounds, upperbounds);
         erfüllt den Zweck ebenfalls
      */

      int ignoreBoundary = (RAND_MAX / count) * count;

      do
      {
         rawNumber = std::[c]rand()[/c];
      } while (rawNumber > ignoreBoundary);

      return lowerbounds + rawNumber % (upperbounds - lowerbounds + 1);
   }

Zunächst prüft die Funktion rnd_nobias() , ob die Mächtigkeit des Wertebereichs eine Zweierpotenz ist, in diesem Fall wird die normale Funktion verwendet. Ansonsten wird eine Grenze berechnet, die angibt***,*** ab welchem Schwellwert die unbewerteten Zufallszahlen von rand() verworfen werden. Liegt eine Zahl über diesem Schwellwert, wird die Berechnung wiederholt. Dies geschieht solange, bis die gezogene Zahl unter dem Schwellwert liegt.

***Implementierungs***technisch ist das übrigens nicht ganz unbedenklich, da hier eigentlich nicht mehr sichergestellt ist, wie lange die Funktion für die Ermittlung der Zahl benötigt, der Funktionsaufruf kann mit einer gewissen (kleinen) Wahrscheinlichkeit sehr lange dauern. Für Echtzeitanwendungen kann dies problematisch sein.

Größere Zufallszahlen

Bisher gilt immer noch die Einschränkung, dass man keine größeren Zufallszahlen als aus einem Intervall der maximalen Mächtigkeit von RAND_MAX ziehen kann. Eine Ziehung einer Zufallszahl zwischen 1 und 1.000.000 ist mit rand() nicht direkt möglich.

Jetzt muss man ein bisschen nachdenken, wie man dieses Ziel doch erreichen kann. rand() liefert maximal 32768 Zufallszahlen, also letztlich 15 zufällige Bits. 1.000.000 benötigt zur binären Darstellung 20 Bits (2^20 = 1.048.576). Was liegt also näher, als hier die Bits von zwei aufeinander folgenden rand() -Ergebnissen miteinander zu kombinieren? Von der ersten Ziehung nimmt man 15 zufällige Bits, und von der zweiten Ziehung die restlichen 5 Bits – und fertig ist eine Zufallszahl im Bereich von 0 bis 1.048.575. Die danach mit Modulo % 1000000 zurecht geschnitten wird.

#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;

int main()
{
   std::srand(static_cast<int>(std::time(NULL)));

   for (unsigned u = 0; u < 20; u++)
   {
      int rnd1 = [c]rand()[/c];
      int rnd2 = [c]rand()[/c];
      int bigrnd = ((rnd1 & 0x1F) << 15) | rnd2;

      cout << bigrnd % 1000000 + 1<< endl;
   }

   return 0;
}

Betrachten Sie die Zusammensetzung der Zahl bigrnd : der Ausdruck rnd1 & 0x1F schneidet die letzten 5 Bit (0x1F entspricht binär 11111) ab (die höheren Bits werden auf 0 gesetzt). Danach wird das Ergebnis um 15 Stellen nach links geschoben, und in den freien Raum rechts wird die Zahl rnd2 komplett – also mit allen 15 Bits – verodert (man könnte statt dem binären Oder auch addieren, das macht in diesem Fall keinen Unterschied, da der Bereich mit Nullen gefüllt ist).

Das ist bereits fast gut. Allerdings müssen Sie an dieser Stelle wieder zur Abbildung 2 zurückgehen und über den Einfluss der Störung nachdenken. Je näher die maximale Zahl an der maximal verfügbaren größten Zahl dran ist, desto größer wird die Störung. Es wäre also besser, wenn man für die Ziehung einer Zufallszahl zwischen 1 und 1.000.000 die Erweiterung nicht nur auf die nächstmögliche Bitgrenze durchführt, sondern darüber hinaus – auf diese Weise reduziert man den Einfluss der ungleichen Häufigkeitsverteilung.

Ein kleiner Hinweis an dieser Stelle: sollte das große Zufallsintervall wieder eine Zweierpotenz sein, so brauchen Sie sich keinen Gedanken über diesen Effekt zu machen, setzen Sie die große Zufallszahl einfach aus den Einzelwerten von rand() zusammen.

Grundsätzlich lässt sich mit diesem hier vorgestellten Kombinationstrick jede Zufallszahl erzeugen, man muss eben ab 30 Bit dreimal rand() aufrufen und kombinieren.

Erweitern Sie nun noch die Klasse Random um eine Zufallszahlerzeugung für rnd32 , also Zufallszahlen im Bereich von 0 bis 4.294.967.296. Das sollte wohl die meisten Wünsche abdecken.

static unsigned int rnd32()
   {
      static Random dummy;
      int rnd1 = [c]rand()[/c];
      int rnd2 = [c]rand()[/c];
      int rnd3 = [c]rand()[/c];
      unsigned int bigrnd = ((rnd1 & 0x03) << 30) + (rnd2 << 15) + rnd3;
   }

Lotto – ganz ohne einstweilige Verfügung

Auch wenn wir zur Zeit online kein Lotto mehr spielen dürfen, soll uns das ja nicht daran hindern, Lottotippgeneratoren zu programmieren. So ein Tippgenerator ist nicht schwer, aber er ist natürlich ein klein wenig kniffliger als ein reines rnd(49) – denn im ersten Schritt zieht man aus 49 Möglichkeiten, dann aus 48, dann aus 47, und so geht das weiter, bis man 6 Zahlen gezogen hat.

Es gibt dafür beliebig viele naive Verfahren – in diesen Fällen sortiert der Programmierer nach jeder Ziehung zum Beispiel ein Array um, oder zieht und prüft, ob er die Zahl bereits gezogen hat. Allen ist gemein, dass sie nicht so effizient sind.

Ein sehr häufig zu findender Ansatz ist die Benutzung der Funktion random_shuffle aus der Klassenbibliothek, die ein vorgegebenes Array durchmischt – und dann nimmt man einfach einen Abschnitt des Arrays. Wie sieht das aus?

#include <iostream>
#include <cstdlib>
#include <ctime>
#include <algorithm>
#include <vector>
#include "random.cpp"
using namespace std;

int main()
{
    srand(static_cast<int>(time(NULL)));
   const unsigned lotto = 49;
   vector<unsigned> numbers(lotto);
   for (unsigned u = 0; u < numbers.size(); u++)
      numbers[u] = u + 1;
   random_shuffle(numbers.begin(), numbers.end());

   for (unsigned u = 0; u < 6; u++)
      cout << numbers[u] << "  ";
   cout << "\n";

   // Sortieren soll auch noch sein? Na gut.
   sort(numbers.begin(), numbers.begin() + 6);
   for (unsigned u = 0; u < 6; u++)
      cout << numbers[u] << "  ";
   cout << "\n";

   return 0;
}

Das ist kurz und knapp, aber für die gesuchte Anwendung nicht optimal, da die Funktion natürlich das gesamte Array durchmischen muss, obwohl eigentlich nur 6 Zahlen gezogen werden sollen.

Übrigens, das Beispiel zeigt Ihnen auch gleich noch, wie man mit Hilfe von sort Teile eines Containers sortieren kann – zwei Iteratoren für Anfang und Ende des Teilarrays sind das notwendige Hilfsmittel.

Vor einiger Zeit wurde dazu im Forum eine sehr schöne Lösung gepostet, so dass es mir natürlich nun schwer fällt***,*** glaubhaft zu machen, dass ich das auf meinem ersten Lottotippgenerator vor 20 Jahren auch schon so programmiert hatte. Wie auch immer, hier die genannte elegantere Lösung.

int main()
{
   const unsigned lotto = 49;
   unsigned numbers[lotto];
   for (unsigned u = 0; u < lotto; u++)
      numbers[u] = u + 1;

   unsigned upperbound = lotto;

   for (unsigned u = 0; u < 6; u++)
   {
      upperbound--;
      unsigned index = Random::rnd(0, upperbound);
      cout << numbers[index] << "  ";
      swap(numbers[index], numbers[upperbound]);
   }

   for (unsigned u = 0; u < 6; u++)
      cout << numbers[43 + u] << "  ";
   cout << "\n";

   return 0;
}

Die Idee ist also, das gezogene Element mit dem Element am Ende des Arrays zu vertauschen, und einfach die Obergrenze der gezogenen Zahl immer schrittweise zu vermindern. Am Ende des Algorithmus stehen dann die 6 gezogenen Zahlen sauber aufgereiht in den Feldern numbers[43] bis numbers[48] .

Jetzt muss nur noch das Glück winken...

Zufälle in der Klassenbibliothek

Die Unterstützung für weitere Zufälligkeiten in der C++-Standardbibliothek ist eher gering – außer der zuvor im Lottobeispiel bereits verwendeten Funktion random_shuffle (aus <algorithm> ) zum Mischen eines Containers findet man hier nichts.

Gerade für statistische Anwendungen benötigt man manchmal spezielle Verteilungen, also ein Ziehungsverhalten des Generators, bei dem bestimmte Zahlenbereiche häufiger oder seltener vorkommen. Denn die vorhandene Generatorfunktion von C++ liefert nur eine Gleichverteilung der Zahlen. Will man hier selbst eingreifen, so kann man dies selbst über ein zwischengeschaltetes Array realisieren. Nehmen Sie an, Sie wollen Zahlen von 1 bis 10 ziehen, aber die geraden Zahlen sollen dabei doppelt so oft vorkommen. So etwas lässt sich mit einer Abbildung einfach erreichen:

unsigned distribution[15];
for (unsigned u = 0; u < 10; u++)
{
   distribution[u] = u + 1;
   if ( (u&1) == 0)
      distribution[10 + u / 2] = u + 2;
}

Dies füllt das Array distribution in der Form:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 2, 4, 6, 8, 10

Und der Aufruf von distribution[rnd() % 15] liefert demnach Zufallszahlen von 1 bis 10, bei denen die geraden Zahlen doppelt so oft vorkommen.

Für komplexere Verteilungsabbildungen, insbesondere wenn es um mathematische Verteilungen geht, sollte man aber doch lieber zu einer Bibliothek greifen – glücklicherweise bietet die „Quasi-Standard-Bibliothek“ boost hier unter dem Namen boost::random zahlreiche Lösungen.

Schlusswort

Wer hätte auf den ersten Blick bedacht, dass selbst eine so kleine und schlichte Funktion wie rand() bereits so viele verborgene Geheimnisse besitzt? Wenn also nun wieder jemand im Forum einmal nach dem besten Weg zur Erzeugung von großen Zufallszahlen fragt, oder mit dem Timer sich selbst Steine in den Weg legt – dann hoffe ich doch, dass Sie diesen Artikel verlinken werden.

Literaturempfehlung

Das Ebook "Numerical Recipes in C", erhältlich unter
http://www.fizyka.umk.pl/nrbook/
http://www.ma.utexas.edu/documentation/nr/bookcpdf/
http://202.38.126.65/mathdoc/Numerical Recipes in C/

Speziell das Kapitel 7:
7 Random Numbers
7.0 Introduction 274
7.1 Uniform Deviates 275
7.2 Transformation Method: Exponential and Normal Deviates 287
7.3 Rejection Method: Gamma, Poisson, Binomial Deviates 290
7.4 Generation of Random Bits 296
7.5 Random Sequences Based on Data Encryption 300
7.6 Simple Monte Carlo Integration 304
7.7 Quasi- (that is, Sub-) Random Sequences 309
7.8 Adaptive and Recursive Monte Carlo Methods 316

Marc++us

Zufälle gibt's!

Der folgende Artikel soll gerade für Einsteiger an einem Stück das Thema der Zufallszahlen im Computer beleuchten, und viele immer wieder nachgefragten Irrtümer und Fehlannahmen ausräumen.

Albert Einstein schrieb:

Das, wobei unsere Berechnungen versagen,
nennen wir Zufall.

Die Erzeugung von Zufallszahlen am Computer ist ein beliebtes Beispiel, das einem in jedem Programmierkurs irgendwann begegnet. Aber das obige Zitat von Albert Einstein deutet bereits das Grundproblem an, dem man am Computer bei der Erzeugung von Zufallszahlen begegnen wird: der Computer kann nur rechnen. Ohne zu versagen. Ist dann die Erzeugung von zufälligen Zahlen am Computer nicht bereits ein Widerspruch?

Bevor wir uns mit dieser schon fast philosophischen Frage befassen, beginnen wir mit den Grundlagen der Zufallszahlen in den heute typischen Programmiersprachen.

Der Würfel ist gefallen

In der Bibliothek cstdlib befindet sich die Funktion rand() , die freundlicherweise eine Zufallszahl zwischen 0 und einer Konstante RAND_MAX liefert. Diese Konstante hat üblicherweise den Wert 32767 – offensichtlich lassen sich mit dieser Funktion keine Zufallszahlen erzeugen, die größer sind, also zum Beispiel zwischen 0 und 1000000. Diesem Problem widmen wir uns aber später.

Die andere Frage ist, wie man die zurückgelieferte Zahl auf den gewünschten Wert zuschneidet; ein Würfel oder ein Münzwurf brauchen ja Zufallszahlen in einem Bereich von 1…6 oder 0 und 1, man muss den Wertebereich also anpassen. Die Mathematik bietet dafür die Möglichkeit, den Modulus einer Zahl zu berechnen, das ist der Rest, der bei einer Division durch eine Ganzzahl übrig bleibt. Wikipedia weiß einiges dazu

http://de.wikipedia.org/wiki/Modulo_(Rest)

- aber das schreit nach einem Beispiel:

#include <iostream>
using namespace std;

int main()
{
   for (unsigned u = 0; u < 20; u++)
   {
      cout << u << "\t" << (u % 6) << endl;
   }

   return 0;
}

Dieses kleine Programm zählt von 0 bis 19, in der linken Spalte steht die Zahl, in der rechten Spalte jeweils die Zahl Modulus 6 – in C und C++ wird dies als u % 6 geschrieben. Damit ist es also möglich, das Intervall der gelieferten Zahl wunschgemäß zu beschneiden. Dass die Zahlen immer auf den Bereich 0 bis 5 zugeschnitten werden, sollte nicht weiter stören, eine Addition von 1 wird den Bereich auf 1 bis 6 anheben. Lassen wir nun ein Programm würfeln.

#include <iostream>
#include <cstdlib>
using namespace std;

int main()
{
   for (unsigned u = 0; u < 20; u++)
   {
      cout << 1 + [c]rand()[/c] % 6 << endl;
   }

   return 0;
}

Wunderbar! 20mal wird nun gewürfelt, alle Zahlen liegen zwischen 1 und 6. Gäbe es mit diesem Programm nicht ein paar kleine Probleme, wäre die Sache bereits als gelöst zu betrachten.

Eine allgemeine Formel für Werte aus einem bestimmten Bereich

Zunächst sollte aber dieses Zwischenergebnis festgehalten werden – um eine Zufallszahl zwischen zwei Grenzen a und b zu erhalten, kann man immer die folgende Berechnung verwenden:

zahl = a + [c]rand()[/c] % (b – a + 1);

Für einen Münzwurf – wo nur Zahlen zwischen 0 und 1 benötigt werden – ergibt sich daraus:

zahl = 0 + [c]rand()[/c] % (1 – 0 + 1);

also

zahl = [c]rand()[/c] % 2;

In eine Funktion random gepackt, ergibt sich dieses Beispiel (diesmal müssen die Lottozahlen herhalten):

#include <iostream>
#include <cstdlib>

int random(int lowerbounds, int upperbounds)
{
   return lowerbounds + std::[c]rand()[/c] % (upperbounds - lowerbounds + 1);
}

using namespace std;

int main()
{
   for (unsigned u = 0; u < 20; u++)
   {
      cout << random(1, 49) << endl;
   }

   return 0;
}

Da ist nur noch eine kleine Kleinigkeit anzumerken... die Differenz der beiden Grenzen darf natürlich nicht größer RAND_MAX werden. Denn da die Funktion rand() nur Zahlen zwischen 0 und RAND_MAX liefert, kann ein größeres Intervall mit diesem Ansatz nicht abgedeckt werden. Eine Erweiterung der Funktion random() um eine entsprechende Sicherheitsprüfung ist sinnvoll:

#include <cassert>

int random(int lowerbounds, int upperbounds)
{
   assert(upperbounds - lowerbounds < RAND_MAX);
   return lowerbounds + std::[c]rand()[/c] % (upperbounds - lowerbounds + 1);
}

Sollte diese Bedingung irgendwann einmal verletzt sein, wird das Programm an dieser Stelle eine Assertion anzeigen. Übrigens, es ist mit dieser Funktion durchaus möglich, Zahlen aus einem größeren Wertebereich zu erzeugen, oder auch negative Zahlen. Gültig ist also:

zahl = random(-10, 10);
   zahl = random(100000, 110000);

Nur die Bedingung des Wertebereichs darf nicht verletzt werden, die Lage der Grenzen selbst innerhalb des Zahlenraums von int spielt keine Rolle.

Eine Formel, die würfelt

Wiederholen Sie das Würfelprogramm mehrfach:

#include <iostream>
#include <cstdlib>
#include <cassert>

int random(int lowerbounds, int upperbounds)
{
   assert(upperbounds - lowerbounds < RAND_MAX);
   return lowerbounds + std::[c]rand()[/c] % (upperbounds - lowerbounds + 1);
}

using namespace std;

int main()
{
   for (unsigned u = 0; u < 20; u++)
   {
      cout << random(1, 6) << endl;
   }

   return 0;
}

Ganz schön einfallslos, unser Gegenspieler – egal wie oft das Programm gestartet wird, immer legt es mit der Zahlenfolge 6, 6, 5, 5, 6, 5, usw., los. Warum ist das so? Gehen wir zu Albert Einstein zurück – der Computer kann eben nicht würfeln, folglich rechnet er. Würden Sie in die Funktion rand() innerhalb der Bibliothek schauen, so fänden Sie dort folgende Zeilen (je nach Compiler kann die genaue Form etwas anders aussehen, das Prinzip bleibt aber immer gleich):

static long holdrand = 1L;
int rand(void)
{
   return (((holdrand = holdrand * 214013L + 2531011L) >> 16) & 0x7fff);
}

Wo ist denn hier der Zufall? Eine simple Formel… ein paar seltsame Zahlen… das war's bereits. Man kann sehen, dass das Ergebnis der Berechnung nicht nur zum Aufrufer zurückgegeben wird, sondern auch in der statischen Variablen holdrand gesichert wird. Offensichtlich realisiert diese Funktion also eine Iteration, jedes Ergebnis hängt immer vom Ergebnis des Vorgängers ab. Aber beim Programmstart beginnt immer alles mit dem gleichen Startwert, denn holdrand wird mit 1 initialisiert (dieser Startwert wird bei einem Zufallszahlengenerator übrigens Seed genannt). Offensichtlich ist das alles ein großer Bluff, denn eine Formel gaukelt nur zufällige Zahlen vor, und wenn man das Programm wiederholt startet, liefert die Formel immer und immer wieder die gleichen Zahlen.

Die hier vorgestellte Formel basiert auf der Methode der linearen Kongruenz, die 1951 von Lehmer vorgestellt wurde, um N Zufallszahlen zu erstellen:

a[0] = seed;
for (i = 1; i <= N; i++)
   a[i] = (a[i – 1] * b + 1) % m;

Die Auswahl der richtigen Zahlen für seed, b und m ist keine triviale Aufgabe, denn die Formel muss gewisse Bedingungen erfüllen, die man an mathematische Zufallszahlen stellt:

Wenn man sehr oft die Formel wiederholt, sollen alle Zahlen mit der ungefähr gleichen Verteilung gezogen werden
Die Zahlen sollen in beliebiger Reihenfolge erscheinen

Für diese Zufallszahlengeneratoren gibt es zahlreiche statistische Tests, die die Bedingungen überprüfen. Glück für uns, dass jemand die Tests für die Funktion rand() in der Standardbibliothek bereits ausgeführt hat, und dass geeignete Werte für b und m gefunden wurden.
Robert Sedgewick gibt in seinem Buch "Algorithmen in C" einen Einblick in die Thematik der Erzeugung von eigenen Zufallszahlenformeln. Auch Donald E. Knuth widmet sich in seinem "The Art Of Computer Programming, Vol. 2" diesem Thema.

Algorithmen in C | ISBN: 3827371821
The art of computer programming | ISBN: 0201896842

Kommen wir wieder zurück zur Praxis: wir wissen nun, warum nach jedem Programmstart immer die gleichen Zahlen erscheinen. Aber gelöst ist das Problem immer noch nicht.

Zeiten und Zufälle

Lustigerweise ist die Lösung für dieses Problem höchstwahrscheinlich wesentlich älter als Sie, lieber Leser, es sind.

Ein Rückblick ins Jahr 1981. Im BASIC-Handbuch des Sinclair ZX81, einem 8-Bit-Rechner mit Folientastatur und 1kB RAM, findet sich folgende Passage:

RAND
RAND <startwert>

Mit RAND können Sie einen neuen Startwert für die Zufallszahlenberechnung mit RND festlegen. Der gleiche Startwert führt immer zur gleichen Folge von Zufallszahlen. So etwas wie "echte" Zufälligkeit erreichen Sie mit "RAND 0". Dabei wird der Startwert aus der Laufzeit des Computers ermittelt.

Um also zufälliger zu werden, brachte man eine Zeit ins Spiel. Die Überlegung ist, dass je nach Laufzeit des Computers der interne Timer einen anderen Wert hat. Den gerade aktuellen Wert des Timers verwendet man nun als Startwert der Zufallsgeneratorfolge – die Wahrscheinlichkeit einer Wiederholung wird nun fast auf 0 gebracht, da selbst nach einem Einschalt- und Bootvorgang nie die gleiche Zeit erreicht wird, ein kleiner Zeitunterschied stellt sich immer ein. Und den Startwert des Zufallszahlengenerators, den Seed, kann man in C++ mit der Funktion srand() setzen.

Erweitern Sie das letzte Würfelprogramm um zwei Zeilen, und staunen Sie:

#include <ctime>  // <-- Neu

...

int main()
{
   srand(static_cast<int>(time(NULL)));  // <-- Neu
   for (unsigned u = 0; u < 20; u++)
   {
      cout << random(1, 6) << endl;
   }

   return 0;
}

Endlich, nach mehrfachem Starten des Programms ergibt sich jedes Mal eine andere Zahlenfolge.

Viel hilft viel – nicht immer

Auf eine böse Falle will ich noch hinweisen, es handelt sich hier um einen beliebten Fehler, den man überraschend oft in Programmen findet. Wohlmeinende Programmierer setzen nämlich vor jeder Ziehung den Startwert aus der Zeit erneut. Werden aber nun Zahlen schneller gezogen als die Uhr tickt, erhalten Sie statt vieler unterschiedlicher Zahlen plötzlich immer den gleichen Wert. Das ist umso dramatischer, da time() ein Sekundentimer ist, und innerhalb einer Sekunde kann man ziemlich oft eine Zufallszahl ziehen.

Probieren Sie es einmal aus.

#include <iostream>
#include <cstdlib>
#include <ctime>
#include <cassert>

int random(int lowerbounds, int upperbounds)
{
   assert(upperbounds - lowerbounds < RAND_MAX);
   return lowerbounds + std::[c]rand()[/c] % (upperbounds - lowerbounds + 1);
}

using namespace std;

int main()
{
   for (unsigned u = 0; u < 20; u++)
   {
      srand(static_cast<int>(time(NULL)));
      cout << random(1, 6) << endl;
   }

   return 0;

Gegen so einen Zufall spielt man gerne! Sehr leicht ist zu sehen, dass immer die gleiche Zahl angezeigt wird – wenn Sie richtig viel Glück haben (man kann dann von Zufall sprechen) erwischen Sie gerade den Sekundenwechsel innerhalb von time() , dann sehen Sie zwei Zahlen. Aber nun ist es wieder vorbei mit dem Zufall. Der wiederholte Aufruf der Funktion srand() setzt die Formel immer wieder auf den gleichen Startwert, da sich die Zeit nicht schnell genug ändert.

Die Klasse für den Zufall

Es ist ja reichlich unhandlich, immer irgendwo das srand() im Programm zu platzieren, damit es nicht vergessen wird. Auch haben Sie ja bereits gelernt, wie man Zufallszahlen in einem Intervall erzeugt. Es wäre an der Zeit, das nun in eine kleine handliche Hilfsklasse zu packen, so dass sie für eigene Programme immer zur Verfügung steht.

// Datei: random.cpp
#ifndef _RANDOM_H
#define _RANDOM_H

#include <cstdlib>
#include <ctime>
#include <cassert>

class Random
{
private:
   Random()
   {
      std::srand(static_cast<int>(std::time(NULL)));
   }
public:
   static int rnd(int lowerbounds, int upperbounds)
   {
      static Random dummy;
      assert(upperbounds - lowerbounds < RAND_MAX);
      return lowerbounds + std::[c]rand()[/c] % (upperbounds - lowerbounds + 1);
   }
};

#endif

Die Klasse wendet einen kleinen Trick an, um den Zufallszahlengenerator zu initialisieren. Die Initialisierung soll nur ein einziges Mal durchgeführt werden, vor dem ersten Aufruf der Memberfunktion rnd() . Dies kann dadurch erreicht werden, dass man innerhalb von rnd() eine statische Variable anlegt, diese wird ganz zu Beginn des Programms initialisiert. Das Dumme ist nur, dass srand() leider keinen return-Wert hat, die an sich nahe liegende Konstruktion dummy = srand(time(NULL)) verbietet sich daher. Als Lösung wird srand() im privaten Konstruktor von Random verkapselt, und innerhalb der Funktion rnd() wird ein statisches Objekt von Random angelegt. Vor der ersten Ausführung von rnd() wird daher garantiert der Konstruktor Random::Random aufgerufen, und damit der Zufallszahlengenerator über die Zeit initialisiert.

Als Demoprogramm spielen wir diesmal Schere, Stein, Papier:

#include <iostream>
#include "random.cpp"

using namespace std;

int main()
{
   char* hand[] = {"Schere", "Stein", "Papier"};

   for (unsigned u = 0; u < 20; u++)
   {
      cout << hand[Random::rnd(0, 2)] << endl;
   }

   return 0;
}

Der Blick über den Tellerrand

Zwei Programmiersprachen, bei denen man Zufallszahlen mit der Zeit initialisieren muss, kennen Sie nun schon: das BASIC des ZX81, und C++. Sie können sich leicht denken, dass auch C sich gleich verhält. Wie sieht es mit anderen Sprachen aus?

In PHP wurde ab der Version 4.2.0 eine interne Erweiterung durchgeführt, seitdem muss vor dem Aufruf von rand() kein srand() mehr ausgeführt werden. Bei älteren Versionen ist auch weiterhin die Zeitinitialisierung notwendig:

<? php
   srand((double)microtime()*1000000); // vor Version 4.2.0
   for($i = 0; $i < 10; $i++)
   {
      $Zufallszahl = rand(0, 100);
      echo ($Zufallszahl."<br/>");
   }
?>

Java stellt eine Klasse Random zur Verfügung, die über zwei Konstruktoren verfügt:

public Random();
public Random(long seed);

Erzeugt man das Objekt der Klasse mit dem parameterlosen Konstruktor, also in dieser Form:

Random rnd = new Random();

so wird das Objekt ebenfalls mit der Systemzeit initialisiert. Als Alternative kann man dem Konstruktor einen eigenen Startwert übergeben.

Auch beim Entwurf von .NET hat Microsoft an dieses Thema gedacht, und erlaubt eine automatische Initialisierung der Klasse System.Random , ohne dass sich der Programmierer darum kümmern muss:

Random rnd = new Random();
int Zufallszahl = rnd.Next(1, 6);

Somit sind die Programmierer der Sprachen C# und VB.NET ebenfalls von der Last befreit, an die Zeitinitialisierung zu denken.

Es gibt übrigens noch andere Möglichkeiten, einen Startwert zu setzen, als auf Zeiten zurückzugreifen. Manche Verschlüsselungsprogramme oder Applets für Online-Banking verwenden zufällige Mausbewegungen oder Tastatureingaben, das Programm misst den Verfahrweg der Maus über eine gewisse Zeit, oder die Dauer zwischen den Tastenanschlägen bei der Eingabe, und generiert daraus einen Startwert. Das ergibt durchaus Sinn, denn gerade solche Programme müssen sich einer Reproduzierbarkeit auf jeden Fall entziehen, würde man sich hier nur auf einen sekundenbasierten Systemtimer verlassen, wäre die Möglichkeit der Manipulation gegeben.

Verteilungsgerechtigkeit

Gemäß der Ausführungen zur Formel, die die Zufallszahlen generiert, sind die Zahlen weitgehend gleichmäßig verteilt. Nehmen wir zunächst also als Voraussetzung an, dass unsere Funktion rand() das Gesetz der großen Zahl tatsächlich erfüllt, und wir bei 1 Billion Ziehungen alle Zahlen gleich oft erhalten.

An dieser Stelle kommt nun ein möglicherweise unangenehmer Effekt zum Tragen, der aus dem Abschneiden der Zufallszahlen kommt. Nehmen Sie das Beispiel Schere, Stein, Papier. Benötigt werden nur Zufallszahlen von 0 bis 2, drei Stück an der Zahl. Erzeugen können wir Zahlen von 0 bis RAND_MAX (32767), das sind genau 32768 unterschiedliche Werte. Und diese Zahl ist nicht durch drei teilbar. Um das Problem zu verstehen, betrachten Sie dieses Programm:

#include <iostream>
using namespace std;

int main()
{
   for (unsigned u = 0; u <= RAND_MAX; u++)
   {
      cout << u << "\t" << u % 3 << endl;
   }
   return 0;
}

Am Anfang geht's noch sauber los:

aber am Ende ist ein kleines Problem vorhanden:

Es geht nicht auf! Der größtmögliche Wert 32767 – der Zufallszahlengenerator schneidet wegen &0xffff alles darüber ab – wird durch das Modulo 3 auf 1 gesetzt. Sie können sich das wie das Ablegen von Kugeln vorstellen, man legt immer reihum in die drei Töpfe; zählt man am Ende die Kugeln in den drei Töpfen 0, 1 und 2, so liegt diese Anzahl von Kugeln pro Topf vor:

Topf 0:   10923   33,33435%
Topf 1:   10923   33,33435%
Topf 2:   10922   33,33130%

Der Unterschied ist noch nicht so dramatisch und wirkt sich erst in der 5ten Stelle aus, aber offensichtlich würde die Schere-Stein-Papier-Software das Papier (da Topf 2 auf Papier abgebildet wird) geringfügig seltener ziehen. Spielt das Programm gegen einen menschlichen Spieler, so wird bei der geringen Anzahl an Ziehungen dieser Effekt gar nicht auffallen. Handelt es sich aber um eine viele millionenmal wiederholte Ziehung für eine Simulation, kann sich diese Bevorzugung irgendwann bemerkbar machen. Man kann diesen Effekt dramatisch vergrößern, wenn die Zufallszahlen nicht aus einem kleinen Intervall stammen müssen, sondern aus einem sehr großen. Nehmen Sie an, Sie benötigen für eine Simulation Zufallszahlen zwischen 0 und 9999. Lassen Sie uns mit einem Programm zählen, wie viele Kugeln in welcher Kiste landen.

#include <iostream>
using namespace std;

int main()
{
   int topf[10000];
   for (int i = 0; i < 10000; i++)
      topf[i] = 0;

   for (unsigned u = 0; u < RAND_MAX; u++)
   {
      topf[u % 10000]++;
   }

   cout << topf[0] << endl;
   cout << topf[9999] << endl;

   return 0;
}

Wir verzichten auf die Ausgabe aller 10000 Töpfe, aber bereits diese Ausgabe sollte Sie schockieren:

4
3

Eine satte Abweichung von 33%. Das ist auch klar: Zahlen ab 30000 werden wieder in die ersten Töpfe abgebildet, aber ab der Zahl 32768 gibt's keine weiteren Zahlen mehr, der Generator erzeugt wieder Zahlen ab 0, die ebenfalls in die ersten Töpfe "geworfen" werden. Daraus ergibt sich ein massives Ungleichgewicht. Wo ist die Grenze? Nun, die lässt sich leicht berechnen (32768 – 3 * 10000 – 1), sie liegt beim Topf 2767, ergänzen Sie noch die Ausgabe um:

cout << topf[2766] << endl;
   cout << topf[2767] << endl;

Folglich erhalten die ersten 2767 Töpfe (als etwa ein Viertel) im Einzelvergleich 33% mehr Treffer als die restlichen Töpfe. Das auf diese Art und Weise erzeugte "zufällige" System hat einen deutlichen Drall. Ob dies in der Anwendung störend ist kann man pauschal nicht sagen, dafür müsste man schon das Anwendungsgebiet kennen. Aber eine Simulation kann hier bereits deutliche und ungewollte Verzerrungen erfahren.

In der folgenden Abbildung sehen Sie die Auswirkung bei den ersten 100 Zahlen.

Offensichtlich ist hier, dass die Störung, also die Abweichung der Häufigkeit zwischen der um eins häufiger gezogenen Zahl und den benachteiligten Zahlen, mit zunehmender Größe des Zahlenintervalls zunimmt. Aber auffallend sind die Lücken, die bei den Zahlen 2, 4, 8, 16, 32 und 64 liegen. Dies gilt auch allgemein: bei den Zweierpotenzen gibt es diese Abweichung nicht, da in diesen Fällen 32768 genau ohne Rest durch die Zahl teilbar ist. Und da es keinen Rest, keinen Überlauf, gibt, wird auch kein Topf bevorzugt.

Betrachtet man die gesamte Darstellung für alle möglichen Intervallgrößen, ergibt sich ein relativ dramatisches Bild:

Für sehr große Intervalle wird die Störung extrem, sie liegt bei 100% - im Klartext heißt das, dass die unteren Töpfe im Extremfall doppelt so viele Zahlen erhalten wie die oberen. Aber auch hier sieht man die Lücken bei 4096, 8192 und 16384.

Mehr Gerechtigkeit

Ein erkanntes Problem ist schon fast ein gelöstes Problem. Es gibt drei grundsätzliche Möglichkeiten, mit dieser Ungleichverteilung umzugehen:

Sie ignorieren es, weil es in Ihrer Anwendung vernachlässigbar ist und keine Auswirkung hat
Sie haben kein Problem damit, da die Anzahl der benötigten Zufallszahlen eine Zweierpotenz ist. (Tipp: falls Sie einen Algorithmus entwerfen, der ein größeres Intervall an Zufallszahlen benötigt, ist es daher auch sinnvoll, diesen so zu gestalten, dass die Anzahl benötigter Zufallszahlen einer Zweierpotenz entspricht.)
Sie dürfen die Zahlen aus dem Endbereich des Zufallszahlengenerators nicht berücksichtigen. Dafür folgt sogleich ein Implementierungsbeispiel.

Wir erweitern unsere Klasse Random , so dass mit einer zusätzlichen Funktion die Ungleichverteilung nicht mehr stattfinden kann.

static int rnd_nobias(int lowerbounds, int upperbounds)
   {
      static Random dummy;
      assert(upperbounds - lowerbounds < RAND_MAX);

      int rawNumber;
      int count = upperbounds - lowerbounds + 1;

      if (count == 2 || count == 4 || count == 8 || 
          count == 16 || count == 32 || count == 64 || 
          count == 128 || count == 256 || count == 512 || 
          count == 1024 || count == 2048 || count == 4096 || 
          count == 8192 || count == 16384)
          return rnd(lowerbounds, upperbounds);

      /* dieser Programmabschnitt kann auch noch eleganter formuliert
         werden, allerdings ist dann die Wirkung nicht mehr auf den
         ersten Blick erkennbar:
      if ((count - 1) & count == 0)
          return rnd(lowerbounds, upperbounds);
         erfüllt den Zweck ebenfalls
      */

      int ignoreBoundary = (RAND_MAX / count) * count;

      do
      {
         rawNumber = std::[c]rand()[/c];
      } while (rawNumber > ignoreBoundary);

      return lowerbounds + rawNumber % (upperbounds - lowerbounds + 1);
   }

Zunächst prüft die Funktion rnd_nobias() , ob die Mächtigkeit des Wertebereichs eine Zweierpotenz ist, in diesem Fall wird die normale Funktion verwendet. Ansonsten wird eine Grenze berechnet, die angibt, ab welchem Schwellwert die unbewerteten Zufallszahlen von rand() verworfen werden. Liegt eine Zahl über diesem Schwellwert, wird die Berechnung wiederholt. Dies geschieht solange, bis die gezogene Zahl unter dem Schwellwert liegt.

Implementierungstechnisch ist das übrigens nicht ganz unbedenklich, da hier eigentlich nicht mehr sichergestellt ist, wie lange die Funktion für die Ermittlung der Zahl benötigt, der Funktionsaufruf kann mit einer gewissen (kleinen) Wahrscheinlichkeit sehr lange dauern. Für Echtzeitanwendungen kann dies problematisch sein.

Größere Zufallszahlen

Bisher gilt immer noch die Einschränkung, dass man keine größeren Zufallszahlen als aus einem Intervall der maximalen Mächtigkeit von RAND_MAX ziehen kann. Eine Ziehung einer Zufallszahl zwischen 1 und 1.000.000 ist mit rand() nicht direkt möglich.

Jetzt muss man ein bisschen nachdenken, wie man dieses Ziel doch erreichen kann. rand() liefert maximal 32768 Zufallszahlen, also letztlich 15 zufällige Bits. 1.000.000 benötigt zur binären Darstellung 20 Bits (2^20 = 1.048.576). Was liegt also näher, als hier die Bits von zwei aufeinander folgenden rand() -Ergebnissen miteinander zu kombinieren? Von der ersten Ziehung nimmt man 15 zufällige Bits, und von der zweiten Ziehung die restlichen 5 Bits – und fertig ist eine Zufallszahl im Bereich von 0 bis 1.048.575. Die danach mit Modulo % 1000000 zurecht geschnitten wird.

#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;

int main()
{
   std::srand(static_cast<int>(std::time(NULL)));

   for (unsigned u = 0; u < 20; u++)
   {
      int rnd1 = [c]rand()[/c];
      int rnd2 = [c]rand()[/c];
      int bigrnd = ((rnd1 & 0x1F) << 15) | rnd2;

      cout << bigrnd % 1000000 + 1<< endl;
   }

   return 0;
}

Betrachten Sie die Zusammensetzung der Zahl bigrnd : der Ausdruck rnd1 & 0x1F schneidet die letzten 5 Bit (0x1F entspricht binär 11111) ab (die höheren Bits werden auf 0 gesetzt). Danach wird das Ergebnis um 15 Stellen nach links geschoben, und in den freien Raum rechts wird die Zahl rnd2 komplett – also mit allen 15 Bits – verodert (man könnte statt dem binären Oder auch addieren, das macht in diesem Fall keinen Unterschied, da der Bereich mit Nullen gefüllt ist).

Das ist bereits fast gut. Allerdings müssen Sie an dieser Stelle wieder zur Abbildung 2 zurückgehen und über den Einfluss der Störung nachdenken. Je näher die maximale Zahl an der maximal verfügbaren größten Zahl dran ist, desto größer wird die Störung. Es wäre also besser, wenn man für die Ziehung einer Zufallszahl zwischen 1 und 1.000.000 die Erweiterung nicht nur auf die nächstmögliche Bitgrenze durchführt, sondern darüber hinaus – auf diese Weise reduziert man den Einfluss der ungleichen Häufigkeitsverteilung.

Ein kleiner Hinweis an dieser Stelle: sollte das große Zufallsintervall wieder eine Zweierpotenz sein, so brauchen Sie sich keinen Gedanken über diesen Effekt zu machen, setzen Sie die große Zufallszahl einfach aus den Einzelwerten von rand() zusammen.

Grundsätzlich lässt sich mit diesem hier vorgestellten Kombinationstrick jede Zufallszahl erzeugen, man muss eben ab 30 Bit dreimal rand() aufrufen und kombinieren.

Erweitern Sie nun noch die Klasse Random um eine Zufallszahlerzeugung für rnd32 , also Zufallszahlen im Bereich von 0 bis 4.294.967.296. Das sollte wohl die meisten Wünsche abdecken.

static unsigned int rnd32()
   {
      static Random dummy;
      int rnd1 = [c]rand()[/c];
      int rnd2 = [c]rand()[/c];
      int rnd3 = [c]rand()[/c];
      unsigned int bigrnd = ((rnd1 & 0x03) << 30) + (rnd2 << 15) + rnd3;
   }

Lotto – ganz ohne einstweilige Verfügung

Auch wenn wir zur Zeit online kein Lotto mehr spielen dürfen, soll uns das ja nicht daran hindern, Lottotippgeneratoren zu programmieren. So ein Tippgenerator ist nicht schwer, aber er ist natürlich ein klein wenig kniffliger als ein reines rnd(49) – denn im ersten Schritt zieht man aus 49 Möglichkeiten, dann aus 48, dann aus 47, und so geht das weiter, bis man 6 Zahlen gezogen hat.

Es gibt dafür beliebig viele naive Verfahren – in diesen Fällen sortiert der Programmierer nach jeder Ziehung zum Beispiel ein Array um, oder zieht und prüft, ob er die Zahl bereits gezogen hat. Allen ist gemein, dass sie nicht so effizient sind.

Ein sehr häufig zu findender Ansatz ist die Benutzung der Funktion random_shuffle aus der Klassenbibliothek, die ein vorgegebenes Array durchmischt – und dann nimmt man einfach einen Abschnitt des Arrays. Wie sieht das aus?

#include <iostream>
#include <cstdlib>
#include <ctime>
#include <algorithm>
#include <vector>
#include "random.cpp"
using namespace std;

int main()
{
    srand(static_cast<int>(time(NULL)));
   const unsigned lotto = 49;
   vector<unsigned> numbers(lotto);
   for (unsigned u = 0; u < numbers.size(); u++)
      numbers[u] = u + 1;
   random_shuffle(numbers.begin(), numbers.end());

   for (unsigned u = 0; u < 6; u++)
      cout << numbers[u] << "  ";
   cout << "\n";

   // Sortieren soll auch noch sein? Na gut.
   sort(numbers.begin(), numbers.begin() + 6);
   for (unsigned u = 0; u < 6; u++)
      cout << numbers[u] << "  ";
   cout << "\n";

   return 0;
}

Das ist kurz und knapp, aber für die gesuchte Anwendung nicht optimal, da die Funktion natürlich das gesamte Array durchmischen muss, obwohl eigentlich nur 6 Zahlen gezogen werden sollen.

Übrigens, das Beispiel zeigt Ihnen auch gleich noch, wie man mit Hilfe von sort Teile eines Containers sortieren kann – zwei Iteratoren für Anfang und Ende des Teilarrays sind das notwendige Hilfsmittel.

Vor einiger Zeit wurde dazu im Forum eine sehr schöne Lösung gepostet, so dass es mir natürlich nun schwer fällt, glaubhaft zu machen, dass ich das auf meinem ersten Lottotippgenerator vor 20 Jahren auch schon so programmiert hatte. Wie auch immer, hier die genannte elegantere Lösung.

int main()
{
   const unsigned lotto = 49;
   unsigned numbers[lotto];
   for (unsigned u = 0; u < lotto; u++)
      numbers[u] = u + 1;

   unsigned upperbound = lotto;

   for (unsigned u = 0; u < 6; u++)
   {
      upperbound--;
      unsigned index = Random::rnd(0, upperbound);
      cout << numbers[index] << "  ";
      swap(numbers[index], numbers[upperbound]);
   }

   for (unsigned u = 0; u < 6; u++)
      cout << numbers[43 + u] << "  ";
   cout << "\n";

   return 0;
}

Die Idee ist also, das gezogene Element mit dem Element am Ende des Arrays zu vertauschen, und einfach die Obergrenze der gezogenen Zahl immer schrittweise zu vermindern. Am Ende des Algorithmus stehen dann die 6 gezogenen Zahlen sauber aufgereiht in den Feldern numbers[43] bis numbers[48] .

Jetzt muss nur noch das Glück winken...

Zufälle in der Klassenbibliothek

Die Unterstützung für weitere Zufälligkeiten in der C++-Standardbibliothek ist eher gering – außer der zuvor im Lottobeispiel bereits verwendeten Funktion random_shuffle (aus <algorithm> ) zum Mischen eines Containers findet man hier nichts.

Gerade für statistische Anwendungen benötigt man manchmal spezielle Verteilungen, also ein Ziehungsverhalten des Generators, bei dem bestimmte Zahlenbereiche häufiger oder seltener vorkommen. Denn die vorhandene Generatorfunktion von C++ liefert nur eine Gleichverteilung der Zahlen. Will man hier selbst eingreifen, so kann man dies selbst über ein zwischengeschaltetes Array realisieren. Nehmen Sie an, Sie wollen Zahlen von 1 bis 10 ziehen, aber die geraden Zahlen sollen dabei doppelt so oft vorkommen. So etwas lässt sich mit einer Abbildung einfach erreichen:

unsigned distribution[15];
for (unsigned u = 0; u < 10; u++)
{
   distribution[u] = u + 1;
   if ( (u&1) == 0)
      distribution[10 + u / 2] = u + 2;
}

Dies füllt das Array distribution in der Form:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 2, 4, 6, 8, 10

Und der Aufruf von distribution[rnd() % 15] liefert demnach Zufallszahlen von 1 bis 10, bei denen die geraden Zahlen doppelt so oft vorkommen.

Für komplexere Verteilungsabbildungen, insbesondere wenn es um mathematische Verteilungen geht, sollte man aber doch lieber zu einer Bibliothek greifen – glücklicherweise bietet die „Quasi-Standard-Bibliothek“ boost hier unter dem Namen boost::random zahlreiche Lösungen.

Schlusswort

Wer hätte auf den ersten Blick bedacht, dass selbst eine so kleine und schlichte Funktion wie rand() bereits so viele verborgene Geheimnisse besitzt? Wenn also nun wieder jemand im Forum einmal nach dem besten Weg zur Erzeugung von großen Zufallszahlen fragt, oder mit dem Timer sich selbst Steine in den Weg legt – dann hoffe ich doch, dass Sie diesen Artikel verlinken werden.

Literaturempfehlung

Das Ebook "Numerical Recipes in C", erhältlich unter
http://www.fizyka.umk.pl/nrbook/
http://www.ma.utexas.edu/documentation/nr/bookcpdf/
http://202.38.126.65/mathdoc/Numerical Recipes in C/

Speziell das Kapitel 7:
7 Random Numbers
7.0 Introduction 274
7.1 Uniform Deviates 275
7.2 Transformation Method: Exponential and Normal Deviates 287
7.3 Rejection Method: Gamma, Poisson, Binomial Deviates 290
7.4 Generation of Random Bits 296
7.5 Random Sequences Based on Data Encryption 300
7.6 Simple Monte Carlo Integration 304
7.7 Quasi- (that is, Sub-) Random Sequences 309
7.8 Adaptive and Recursive Monte Carlo Methods 316

Marc++us

@estartu:
Habe ich schon kopiert, keine Sorge.

C++ Forumbot

Dieser Thread wurde von Moderator/in estartu aus dem Forum Die Redaktion in das Forum Archiv verschoben.

Im Zweifelsfall bitte auch folgende Hinweise beachten:
C/C++ Forum :: FAQ - Sonstiges :: Wohin mit meiner Frage?

Dieses Posting wurde automatisch erzeugt.